Lösung von Aufgabe 5.5 P (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br /> <math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> Kategorie:…“) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br /> | Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br /> | ||
<math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> | <math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> | ||
| + | |||
| + | refl: g geschnitten g = g, also nicht {} | ||
| + | symm: Wenn g geschnitten h nicht leer ist, dann ist es andersherum genau so. | ||
| + | tran: Es gibt keine weitere Gerade in der Realtion, aber eine Parallele von g würde von h geschnitten werden, ohne g zu schneiden, was gegen die Transotivität spricht. --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 20:31, 18. Nov. 2018 (CET) | ||
| + | |||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 18. November 2018, 20:31 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
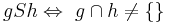
refl: g geschnitten g = g, also nicht {} symm: Wenn g geschnitten h nicht leer ist, dann ist es andersherum genau so. tran: Es gibt keine weitere Gerade in der Realtion, aber eine Parallele von g würde von h geschnitten werden, ohne g zu schneiden, was gegen die Transotivität spricht. --CIG UA (Diskussion) 20:31, 18. Nov. 2018 (CET)

