Lösung von Aufg. 6.5P (WS 18 19): Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
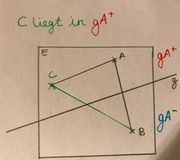
:Eingerückte Zeile Liegt Punkt C in der Halbebene gA+, dann schneidet die Gerade g laut der Definition der Halbebene die Seite BC, aber nicht die Seite AC. | :Eingerückte Zeile Liegt Punkt C in der Halbebene gA+, dann schneidet die Gerade g laut der Definition der Halbebene die Seite BC, aber nicht die Seite AC. | ||
| − | + | [[Datei:GA+.jpg|thumb|Beweis Satz von Pasch]] | |
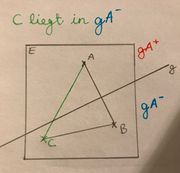
:Eingerückte Zeile Liegt Punkt C in der Halbebene gA-, dann schneidet die Gerade g laut der Definition der Halbebene die Seite AC, aber nicht die Seite BC. | :Eingerückte Zeile Liegt Punkt C in der Halbebene gA-, dann schneidet die Gerade g laut der Definition der Halbebene die Seite AC, aber nicht die Seite BC. | ||
| − | + | [[Datei:GA-.jpg|thumb|Beweis Satz von Pasch]] | |
(Das Gleiche gilt, wenn man statt Seite AB die Seite AC oder die Seite BC als Voraussetzung nutzt.) | (Das Gleiche gilt, wenn man statt Seite AB die Seite AC oder die Seite BC als Voraussetzung nutzt.) | ||
--[[Benutzer:Student01|Student01]] ([[Benutzer Diskussion:Student01|Diskussion]]) 17:14, 21. Nov. 2018 (CET) | --[[Benutzer:Student01|Student01]] ([[Benutzer Diskussion:Student01|Diskussion]]) 17:14, 21. Nov. 2018 (CET) | ||
Version vom 21. November 2018, 17:18 Uhr
Beweisen Sie den Satz von Pasch.
Voraussetzung: g schneidet eine Seite des Dreiecks ABC
Behauptung: g schneidet genau eine weitere Seite des Dreiecks ABC
| Beweisschritt | Begründung |
|---|---|
| 1. g schneidet eine Seite des Dreiecks ABC | Voraussetzung |
| 2. g hat keinen Anfangs und Endpunkt | Def (Gerade) |
| 3. g muss eine weitere Seite des Dreiecks schneiden | Logik, 2. |
anschaulich plausibel aber kein Beweis. Versuchen Sie ohne Anschauung zu argumentieren--Schnirch (Diskussion) 12:12, 21. Nov. 2018 (CET)
Ich habe den Beweis leider nicht in Tabellenform hinbekommen.
Voraussetzung: g schneidet eine Seite des Dreiecks ABC. Behauptung: g schneidet genau eine weitere Seite des Dreiecks ABC.
Beispiel: Voraussetzung: g schneidet Seite AB. Behauptung: g schneidet entweder Seite AC oder Seite BC.
Punkt A teilt die Ebene E in zwei Halbebenen gA+ und gA-. Gerade g schneidet die Seite AB (Voraussetzung). Somit muss die Gerade g entweder die Seite AC oder die Seite BC schneiden (Behauptung).
Es gibt einen Punkt C, der auf der selben Ebene (wie Punkt A und Punkt B) liegen. Somit kann Punkt C entweder in der Halbebene gA+ oder in der Halbebene gA- liegen.
- Eingerückte Zeile Liegt Punkt C in der Halbebene gA+, dann schneidet die Gerade g laut der Definition der Halbebene die Seite BC, aber nicht die Seite AC.
- Eingerückte Zeile Liegt Punkt C in der Halbebene gA-, dann schneidet die Gerade g laut der Definition der Halbebene die Seite AC, aber nicht die Seite BC.
(Das Gleiche gilt, wenn man statt Seite AB die Seite AC oder die Seite BC als Voraussetzung nutzt.)
--Student01 (Diskussion) 17:14, 21. Nov. 2018 (CET)