Lösung von Aufgabe 13.1P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 6: | Zeile 6: | ||
1.) = S<sub>c</sub><math>\circ</math>S<sub>a</sub><math>\circ</math>S<sub>b</sub><math>\circ</math>S<sub>d</sub> '''- b || d (Vor.); Eigenschaft Schubspiegelung'''<br /> | 1.) = S<sub>c</sub><math>\circ</math>S<sub>a</sub><math>\circ</math>S<sub>b</sub><math>\circ</math>S<sub>d</sub> '''- b || d (Vor.); Eigenschaft Schubspiegelung'''<br /> | ||
2.) = S<sub>c</sub><math>\circ</math>S<sub>a</sub><math>\circ</math>S<sub>b'</sub><math>\circ</math>S<sub>d'</sub> mit a=b' und b' || d' und |bd| = |b'd'| '''- 1.) Eig. Verschiebung'''<br /> | 2.) = S<sub>c</sub><math>\circ</math>S<sub>a</sub><math>\circ</math>S<sub>b'</sub><math>\circ</math>S<sub>d'</sub> mit a=b' und b' || d' und |bd| = |b'd'| '''- 1.) Eig. Verschiebung'''<br /> | ||
| − | 3.) = S<sub>c</sub><math>\circ</math>S<sub>d'</sub | + | 3.) = S<sub>c</sub><math>\circ</math>S<sub>d'</sub> '''- 2.), Identität a,b''''<br /> |
4.) = D<sub>P,180</sub> mit c geschnitten d' = P<br /> | 4.) = D<sub>P,180</sub> mit c geschnitten d' = P<br /> | ||
| − | Die Behauptung ist bewiesen. -- | + | Die Behauptung ist bewiesen. --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 12:08, 25. Jan. 2019 (CET) |
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 25. Januar 2019, 12:08 Uhr
Zeigen Sie, dass bei der Verkettung einer Schubspiegelung 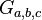 (
(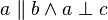 ) mit einer Spiegelung
) mit einer Spiegelung 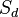 (
(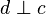 ) eine Punktspiegelung entsteht.
) eine Punktspiegelung entsteht.
Vor: Sa Sb
Sb Sc
Sc Sd mit a || b und a senkrecht zu c und d senkrecht zu c; Beh: = DP,180
Sd mit a || b und a senkrecht zu c und d senkrecht zu c; Beh: = DP,180
1.) = Sc Sa
Sa Sb
Sb Sd - b || d (Vor.); Eigenschaft Schubspiegelung
Sd - b || d (Vor.); Eigenschaft Schubspiegelung
2.) = Sc Sa
Sa Sb'
Sb' Sd' mit a=b' und b' || d' und |bd| = |b'd'| - 1.) Eig. Verschiebung
Sd' mit a=b' und b' || d' und |bd| = |b'd'| - 1.) Eig. Verschiebung
3.) = Sc Sd' - 2.), Identität a,b'
Sd' - 2.), Identität a,b'
4.) = DP,180 mit c geschnitten d' = P
Die Behauptung ist bewiesen. --CIG UA (Diskussion) 12:08, 25. Jan. 2019 (CET)

