Der Schwerpunkt und die Seitenhalbierenden eines Dreiecks: Unterschied zwischen den Versionen
| Zeile 18: | Zeile 18: | ||
== Seitenhalbierende eines Dreiecks == | == Seitenhalbierende eines Dreiecks == | ||
==== Definition Seitenhalbierende eines Dreiecks ==== | ==== Definition Seitenhalbierende eines Dreiecks ==== | ||
| − | Eine Seitenhalbierende eines Dreiecks ist eine Gerade die durch einen Eckpunkt des Dreiecks ABC und den Mittelpunkt der gegenüberliegenden Seite dieses Eckpunktes verläuft.<br />--[[Benutzer:Löwenzahn|Löwenzahn]] 10:36, 21. Jul. 2010 (UTC) | + | Eine Seitenhalbierende eines Dreiecks ist eine Gerade die durch einen Eckpunkt des Dreiecks <math>\overline{ABC}</math> und den Mittelpunkt der gegenüberliegenden Seite dieses Eckpunktes verläuft.<br />--[[Benutzer:Löwenzahn|Löwenzahn]] 10:36, 21. Jul. 2010 (UTC) |
==== Satz: Existenz und Eindeutigkeit der Seitenhalbierende ==== | ==== Satz: Existenz und Eindeutigkeit der Seitenhalbierende ==== | ||
| + | Es existiert zu jeder Seite eines Dreiecks <math>\overline{ABC}</math> genau eine Seitenhalbierende. | ||
===== Teil 1: Existenz ===== | ===== Teil 1: Existenz ===== | ||
Voraussetzung: Dreieck <math>\overline{ABC}</math> mit schulüblichen Bezeichnungen | Voraussetzung: Dreieck <math>\overline{ABC}</math> mit schulüblichen Bezeichnungen | ||
<br />Behauptung: (o.B.d.A) Es existiert eine Gerade <math>\ s_a</math> zwischen dem Mittelpunkt der Seite <math>\ a</math> und dem Punkt <math>\ A</math>. | <br />Behauptung: (o.B.d.A) Es existiert eine Gerade <math>\ s_a</math> zwischen dem Mittelpunkt der Seite <math>\ a</math> und dem Punkt <math>\ A</math>. | ||
| − | + | :(1) Es existiert (genau) ein Punkt <math>\ M_a</math>: Mittelpunkt der Seite a (der Strecke <math>\overline {BC}</math>). | |
| − | + | ::Begründung - Satz III.1: (Existenz '''und Eindeutigkeit''' des Mittelpunkte einer Strecke) | |
| − | + | :(2) Es existiert (genau) eine Gerade <math>\ s_a</math>, die durch die Punkte <math>\ M_a</math> und <math>\ A</math> geht. | |
| − | + | ::Begründung - Axiom I.1: (Axiom von der Geraden) "Zu zwei beliebigen verschiedenen Punkten gibt es '''genau''' eine Gerade, die die beiden Punkte enthält. " | |
===== Teil 2: Eindeutigkeit===== | ===== Teil 2: Eindeutigkeit===== | ||
| − | Da die in Schritt (1) und (2) verwandten Sätze / Axiome von Existenz '''und Eindeutigkeit''' sprechen, ist mit | + | Da die in Schritt (1) und (2) verwandten Sätze / Axiome von Existenz '''und Eindeutigkeit''' sprechen, ist mit dem Existenz-"Beweis" auch die Eindeutigkeit bewiesen. --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 15:32, 21. Jul. 2010 (UTC) |
== Schwerpunkt eines Dreiecks == | == Schwerpunkt eines Dreiecks == | ||
Version vom 21. Juli 2010, 16:40 Uhr
Die Fotos demonstrieren, was unter dem Schwerpunkt eines Dreiecks zu verstehen ist. Erstellen Sie das Skript selbst.
|
|
|---|---|
|
|
|
|
Inhaltsverzeichnis |
Seitenhalbierende eines Dreiecks
Definition Seitenhalbierende eines Dreiecks
Eine Seitenhalbierende eines Dreiecks ist eine Gerade die durch einen Eckpunkt des Dreiecks 
und den Mittelpunkt der gegenüberliegenden Seite dieses Eckpunktes verläuft.
--Löwenzahn 10:36, 21. Jul. 2010 (UTC)
Satz: Existenz und Eindeutigkeit der Seitenhalbierende
Es existiert zu jeder Seite eines Dreiecks genau eine Seitenhalbierende.
Teil 1: Existenz
Voraussetzung: Dreieck mit schulüblichen Bezeichnungen
Behauptung: (o.B.d.A) Es existiert eine Gerade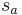 
zwischen dem Mittelpunkt der Seite 
und dem Punkt 
.
- (1) Es existiert (genau) ein Punkt
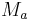: Mittelpunkt der Seite a (der Strecke 
).
- Begründung - Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- (2) Es existiert (genau) eine Gerade 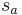, die durch die Punkte 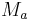und geht.
- Begründung - Axiom I.1: (Axiom von der Geraden) "Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält. "
Teil 2: Eindeutigkeit
Da die in Schritt (1) und (2) verwandten Sätze / Axiome von Existenz und Eindeutigkeit sprechen, ist mit dem Existenz-"Beweis" auch die Eindeutigkeit bewiesen. --Heinzvaneugen 15:32, 21. Jul. 2010 (UTC)
Schwerpunkt eines Dreiecks
Satz: Schnittpunkt der Seitenhalbierende eines Dreiecks
Die Seitenhalbierenden eines Dreiecks schneiden sich in (genau?) einem Punkt.
--Löwenzahn 10:37, 21. Jul. 2010 (UTC)
Definition Schwerpunkt eines Dreiecks
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der Seitenhalbierenden des Dreiecks.--Löwenzahn 10:36, 21. Jul. 2010 (UTC)
