Lösungen Serie 1 WS 20/21: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgabe 1.1 = Definieren Sie die folgenden Begriffe aus der Mengenlehre: {| |- |a)|| Schnittmenge, |- | b)|| Vereinigungsmenge, |- | c)|| Teilmenge, |- | d)|…“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1.1) |
||
| Zeile 12: | Zeile 12: | ||
| d)|| Potenzmenge. | | d)|| Potenzmenge. | ||
|} | |} | ||
| + | ==Lösungen== | ||
| + | ===Lösung 1=== | ||
| + | |||
| + | ===Lösung 2=== | ||
| + | |||
| + | ===Lösung 3=== | ||
| + | |||
| + | =Aufgabe 1.2= | ||
| + | {| | ||
| + | |- | ||
| + | | a)|| Es sei <math>k</math> ein Kreis in Mittelpunktslage bezüglich eines kartesischen Koordinatensystems. Für den Radius <math>r</math> von <math>k</math> gelte <math>r=\sqrt{2}</math>. <math>G</math> sei die Menge aller Koordinatenpaare <math>(x,y)</math> die Punkte von <math>k</math> beschreiben mit <math>x,y \in \mathbb{G}</math>. Geben Sie <math>G</math> in aufzählender Weise an. | ||
| + | |- | ||
| + | | b)|| <math>k_1</math> sei in Kreis mit dem Mittelpunkt <math>M_1=(5,5)</math> und dem Radius <math>r_1=5</math>. <math>k_2</math> sei ein Kreis mit dem Mittelpunkt <math>M_2=(15,15)</math> und dem Radius <math>r_2=\sqrt{125}</math>. Geben Sie die Menge <math>k_1 \cap k_2</math> an. | ||
| + | |} | ||
| + | |||
| + | ==Lösungen== | ||
| + | ===Lösung 1=== | ||
| + | |||
| + | ===Lösung 2=== | ||
| + | |||
| + | ===Lösung 3=== | ||
Version vom 9. November 2020, 11:44 Uhr
Inhaltsverzeichnis |
Aufgabe 1.1
Definieren Sie die folgenden Begriffe aus der Mengenlehre:
| a) | Schnittmenge, |
| b) | Vereinigungsmenge, |
| c) | Teilmenge, |
| d) | Potenzmenge. |
Lösungen
Lösung 1
Lösung 2
Lösung 3
Aufgabe 1.2
| a) | Es sei  ein Kreis in Mittelpunktslage bezüglich eines kartesischen Koordinatensystems. Für den Radius ein Kreis in Mittelpunktslage bezüglich eines kartesischen Koordinatensystems. Für den Radius  von von  gelte gelte 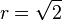 . .  sei die Menge aller Koordinatenpaare sei die Menge aller Koordinatenpaare 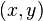 die Punkte von die Punkte von  beschreiben mit beschreiben mit 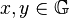 . Geben Sie . Geben Sie  in aufzählender Weise an. in aufzählender Weise an.
|
| b) | 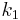 sei in Kreis mit dem Mittelpunkt sei in Kreis mit dem Mittelpunkt 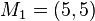 und dem Radius und dem Radius 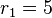 . . 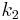 sei ein Kreis mit dem Mittelpunkt sei ein Kreis mit dem Mittelpunkt 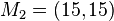 und dem Radius und dem Radius 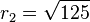 . Geben Sie die Menge . Geben Sie die Menge 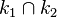 an. an.
|

