Lösung von Aufgabe 13.2: Unterschied zwischen den Versionen
(→Weitere Fragen) |
|||
| Zeile 65: | Zeile 65: | ||
== Weitere Fragen == | == Weitere Fragen == | ||
<br />Habe den Beweis auch so! Stimmt das jetzt oder muss man <ACB so aufteilen, dass zwei rechte Winkel entstehen??!? Bitte um Hilfe der Dozenten!!!!! | <br />Habe den Beweis auch so! Stimmt das jetzt oder muss man <ACB so aufteilen, dass zwei rechte Winkel entstehen??!? Bitte um Hilfe der Dozenten!!!!! | ||
| + | |||
| + | == Anmerkung == | ||
| + | Zu der EP-Diskussion: <br />Ich denke es genüt Def.X.3 (Existenz von Parallelen) aufzuführen, um den Beweis zu führen. Wozu sollten wir die | ||
| + | Eindeutigkeit brauche? Wir brauchen ja nur eine Gerade die Parallel verläuft, dass wir unsere Wechselwinkelsätze anwenden können. | ||
| + | <br /><br /> | ||
| + | Das Problem mit den Nebenwinkeln würde ich wie folgt klären: | ||
| + | Ich nehme mir 2 Winkel davon und fasse sie mit dem Winkeladditionsaxiom zusammen (es gilt dann noch zu begründen, warum der Innere | ||
| + | Strahl auch im inneren liegt). Anschließend kann ich dann mit dem 3. Winkel und dem zusammengefassten Winkel über Nebenwinkel argumentieren. | ||
| + | Anschließen drösle ich den zusammengefassten Winkel wieder auf... Fertig. | ||
| + | <br /> | ||
| + | Beim Wechselwinkelsatz ec. dürfte es aber keine Probleme Geben, da ich mir ja immer nur die 2 Geraden herausnehme, auf die ich mich | ||
| + | beziehe. | ||
| + | |||
| + | --[[Benutzer:TheGeosi|TheGeosi]] 12:53, 24. Jul. 2010 (UTC) | ||
Version vom 24. Juli 2010, 13:53 Uhr
Inhaltsverzeichnis |
Satz XII.4: (Innenwinkelsatz für Dreiecke)
- Es sei
 ein Dreieck mit den Innenwinkeln
ein Dreieck mit den Innenwinkeln 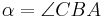 ,
, 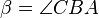 und
und 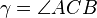 .
.
Es gilt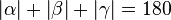 .
.
- Es sei
Versuch 1
VSS: Dreieck  , mit Innenwinkel
, mit Innenwinkel 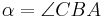 ,
, 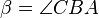 und
und 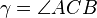
Beh: 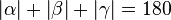
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 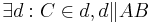
|
(Euklidisches Parallelenaxiom) |
| (II) | 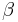 und und 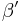 sind Stufenwinkel sind Stufenwinkel
|
(I), (Def. Stufenwinkel) |
| (III) | 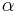 und und 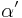 sind Stufenwinkel sind Stufenwinkel
|
(I), (Def. Stufenwinkel) |
| (IV) | 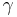 und und 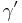 sind Scheitelwinkel sind Scheitelwinkel
|
(I), (Def. Scheitelwinkel) |
| (V) | 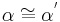 , , 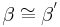
|
(I), (II), (III), (Stufenwinkelsatz) |
| (VI) | 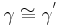
|
(I), (IV), (Scheitelwinkelsatz) |
| (VII) | 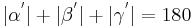
|
(Def. Nebenwinkel), (Supplementaxiom) |
| (VIII) | 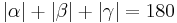
|
(VII), (V), (VI) |
-> Beh. wahr qed
--Löwenzahn 18:07, 16. Jul. 2010 (UTC)
Zum Thema EP
Kommentar --*m.g.* 07:07, 19. Jul. 2010 (UTC): Ich bin mal ganz pingelig. EP sagt aus, dass es durch einen nicht zu  gehörenden Punkt
gehörenden Punkt  höchstens eine Gerade
höchstens eine Gerade  geben kann, die zu
geben kann, die zu  parallel ist. Kann man Schritt (I) wirklich mit EP begründen? Wo kommt EP zum Tragen?
parallel ist. Kann man Schritt (I) wirklich mit EP begründen? Wo kommt EP zum Tragen?
Vorschlag--Heinzvaneugen 08:13, 20. Jul. 2010 (UTC): Über diesen Zusammenhang (die Frage: wozu das EP) haben wir in einer Lerngruppe schon einige Male gesprochen. Ein Vorschlag: das EP braucht man für die EINDEUTIGKEIT von Parallelen - die kann man ohne EP nicht beweisen. Die EXISTENZ von Parallelen kann man allerdings ohne das EP beweisen, das wurde via Umkehrung des Stufenwinkelsatzes bewiesen.
Was hat das mit der Fragestellung zu tun? Wenn man im ersten Schritt behauptet: "es existiert eine Parallele", so kann das mit der Umkehrung des Stufenwinkelsatzes belegt werden. Man müsste sagen: es existiert eine und zwar höchstens eine Parallele und das wird durch die Umkehrung des Stufenwinkelsatzes und das EP bewiesen. Stimmt das so?
Überlegung --Löwenzahn 15:35, 20. Jul. 2010 (UTC): Müsste man dann Schritt (I) mit der Existenz von Parallelen und dem EP begründen? Das EP ist in der Innenwinkelsumme nur wichtig, dass es eben nur eine Parallele gibt... hab ich das so richtig verstanden?
Re: --Heinzvaneugen 19:13, 23. Jul. 2010 (UTC): Fast. Man müsste mit der EINDEUTIGKEIT der Parallelen, die das EP aussagt (höchstens) belegen, dass 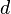 DIE EINZIGE Parallele zu
DIE EINZIGE Parallele zu  durch
durch  ist.
ist. 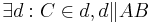 geht, die Begründung sagt aber an, dass man das anders "sprechen" muss: es existiert GENAU EINE Parallele usw. Ganz ordentlich müsste man die Umkehrung des Stufenwinkelsatzes nennen, mit der die EXISTENZ einer Parallelen (...es gibt mindestens eine Parallele...) bewiesen werden kann.
geht, die Begründung sagt aber an, dass man das anders "sprechen" muss: es existiert GENAU EINE Parallele usw. Ganz ordentlich müsste man die Umkehrung des Stufenwinkelsatzes nennen, mit der die EXISTENZ einer Parallelen (...es gibt mindestens eine Parallele...) bewiesen werden kann.
Sind DREI "Neben-" Winkel supplementär?
Und wir haben noch ein Problem: So wie wir Nebenwinkel definiert haben, sprechen wir immer nur von zwei Winkeln, nicht von dreien. Zwei Winkel sind supplementär, wenn sie zusammen 180° ergeben. Sind auch drei Winkel supplementär? Und das gleiche Problem habe ich mit den Scheitel- und Wechselwinkeln. Ich habe den Beweis genauso geführt wie Löwenzahn, aber sicher bin ich da nicht.
--Nicola 12:14, 21. Jul. 2010 (UTC)
Re: Die Begründung ist problematisch, das kann besser mit Winkeladdition erklärt werden. Oder? --Heinzvaneugen 19:13, 23. Jul. 2010 (UTC)
Weitere Fragen
Habe den Beweis auch so! Stimmt das jetzt oder muss man <ACB so aufteilen, dass zwei rechte Winkel entstehen??!? Bitte um Hilfe der Dozenten!!!!!
Anmerkung
Zu der EP-Diskussion:
Ich denke es genüt Def.X.3 (Existenz von Parallelen) aufzuführen, um den Beweis zu führen. Wozu sollten wir die
Eindeutigkeit brauche? Wir brauchen ja nur eine Gerade die Parallel verläuft, dass wir unsere Wechselwinkelsätze anwenden können.
Das Problem mit den Nebenwinkeln würde ich wie folgt klären:
Ich nehme mir 2 Winkel davon und fasse sie mit dem Winkeladditionsaxiom zusammen (es gilt dann noch zu begründen, warum der Innere
Strahl auch im inneren liegt). Anschließend kann ich dann mit dem 3. Winkel und dem zusammengefassten Winkel über Nebenwinkel argumentieren.
Anschließen drösle ich den zusammengefassten Winkel wieder auf... Fertig.
Beim Wechselwinkelsatz ec. dürfte es aber keine Probleme Geben, da ich mir ja immer nur die 2 Geraden herausnehme, auf die ich mich
beziehe.
--TheGeosi 12:53, 24. Jul. 2010 (UTC)

