Lösung von Aufgabe 10.1P (WS 20 21): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Das Dreieck <math>\overline{ABC}</math> wurde durch die Nacheinanderausführung zweier verschiedener Geradenspiegelungen auf das Dreieck <math>\overline{A''B''…“) |
|||
| Zeile 3: | Zeile 3: | ||
<ggb_applet width="649" height="515" version="4.2" ggbBase64="UEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vzdctu2Er5OnwLDi3MVSQT/ROVI6URqfpw4beY4p9M5NxmIhChEFMmSlH8yfZy+SV/sLACSIiVKlmRZodxqbIMgFljg28XuR9B2/8fbuY+uaZywMBgouK0qiAZO6LLAGyiLdNKylR9f/tD3aOjRcUzQJIznJB0oRltTlv2g1rZU3pm5A0WdTDSHqnbLwdhtGbo+aY1N3W1NyMRwbU3Hlu0oCN0m7EUQ/kzmNImIQ6+cKZ2Ty9AhqRhzmqbRi07n5uamnWtvh7HX8bxx+zZxFQQzD5KBkl28gOEqnW50Ia6pKu789vFSDt9iQZKSwKEK4qtasJc/POvfsMANb9ANc9PpQLHMroKmlHlTWKalwpo6XCiCtUbUSdk1TaBrqSrWnM4jRYiRgLc/k1fIL5ajIJddM5fGgE9bVw0DG6oqSwWFMaNBmkniTGMnH6t/zeiNHJRfCX3QKQ1Df0z4eOiPP5Cmaip6zgssCw0Ky5JNqryn6rLQZGHIwpQyhuxuSFFDyhhSxtDB2CxhY58OlAnxE8CPBZMYbFfUk/TOp2I+2Y3l2vFzWFPCvoGwzgGVgMN9VX3OvwHl50aOdGmRuKQ1jRdblcr2ks5co2X0dteoPWideq5Tq1ulZtbrtB+Gba4TmyWdoEp8ie91XK0tKiWQR9aobwN2VeNGU+6h0DJOvURD7XWPvsguBr/pahuVdtVT4Nrv5BGonwUdlEy5bLYpUzpPeBjSe8js8WiCkQkhx+pC8DAR7kHR1RAEGYRNZJhQxTayeNlFehcaDKQjG3E5rCMRc0wbfhhdMZiFTBiM3+1CqEMYFBnI1BEWocpAEKCQCHcQ+jQdJEwTmdCJq8caH0K3kGFBTbeRAXPkka6LQVCHjlAH9RrSMdJ5Z9xFmoUsPh42eAS1bD51GFJDlooszAeEYAmBUgZJkLeRzlcD2yoKE1agO6V+lIMkcGRBtEgr2DlzN79Mw6iwoZB2Q2c2LLDOWihJ0rIYpIllKpJpo5KpnvV9MqY+5PMr7ggIXROfRyqhYRIGKcqdQJP3vJhEU+YkVzRNoVeCvpJrcklSevsGpJNct1AtEmifLhyfuYwEv4KX8CH4gKjIpzz+5vnU0LtSixOGsXt1l4DroNv/0TiEoKkBgyh/IJzeySbdxtUmQDpxCHd6c6UTBJq7DU2WVE2vi6WRW1osCHkxK2zBry+SYei7RXMUsiAdkShdxIIcwexivqhXgedTga1IH0AznNk4vL2SoOpyrM93EdRUOYGxNwr9MEawJTXTBIGsHMtSyPCZFVKqkFGFhJpbiblFO+5pQkKUY1kKKTC7nFq2UpyvEqu5GpZIzqZU3Uw4DWcti4Cll3klZc4sWyqWHX5ezMfgbxlu1THxscbsd1ZcrD+jcUB96UgB2HIRLhLp2YV3PusvEvqJpNNXgfsf6sGe/ER4XExhaCm6nLJLHTaHjvJ+Bh7hhv0vTFXedakX03yJvuCjElrRqpbdeu22GOpNHM4vguvP4DUrU+138vX0EydmEXdONIZAPaNL/3NZQiDMu+V+sPgEVuHwiANAphxEBZFFOg1jQTlh2wLBQO//+jMIaAyBEtgm37E+nQPhRKlwS+HZhXleCR7L7YDC8VeII0XikO1L1KC51kWFMxM/mhLOdTMIfHIHEyiDIsb7GLqrUIElxHogNkTSJyJKpTvJ+cJFBMOJXVgyt8A+QbcDpaXxR5E7/lwC5Tf5XCNZPF8q35qVMCjvrlgNnE6idA9ew/PHC58QrtH5w6VmcGlHgssJ53MSuCgQrO1T6N95YaAs+QJR+a5EBHNnQ0TjIEqEFmneDnHRh8SDpZgjxQgU+kAZS4WZmhr7SIW5BYqhqhkkBVIwgwfSRKS5NEto4uIdc10qKE9nu3FLcJati01d2NfEWYpbmhfvY97NPphQj9eKiTj3eOH+E93TD9e9Sc+8qYW1YrADwAef8LnvXgQ80VGRGtZT44zSiHOSX4LPMQkSfqpTzYm7Q0maA2Ue9ls4w/K8kBw3B8kig7byIGc0GspqjvlpHcgqBT2DJKOfMCe/Pi1ev0wmCU0F8bBkItVOhSY+AZpvnoD3mStJ6RQU5yfJXV5L7vJmE8XRpNhEirmS4tCDKI52HIpTtW5jOM7kPj88YT7J95+ak5xeo9PJKpRug6AsUvN5ZOZVKGmToMSrLAfjRoNZTTRvn0CiyZ3ZPEFifveE8FLb9iMk5ktw+pWs/Fam23dr6djbnnL5/imA9Q7c9NWD7yPsePFrC+U8ZLeNw/c7/T2QXRJ5fs3mkc8clu7jlBdPwCnzMGo9ClusccoL6ZRv15xyuodTTpvilDl8+cNJq/uQJLSrU1ZB/sjiOIzrDx29NZhf/YtEYfLv+0h35bVC1uX7evsSdGv5fF354Efw4Fpwh5vAHe4P7rBh4GrtXvVjHfUsYwd0R5vQHe2P7qhh6BrLB4Dqxzjd64gMEvlSoqhoFXxrX1CUOzrljqSo8FcWu1mp/sVFyVxP9dne2c0lH3m+Zae027aNu7aBe10IopqpvW5lp3stfYOfntfpPGkc5Lg+yuJ6uFtYPSu8x43Du1UXcBt8ELMLwyuH4+kmnncw29tkwkd84798uWDL3WA+iLIc64XBLoRwuy2Gh9pi+N1sscOB8Ckp4XZ8R4fiO2oivqUXON+ZI9YwxRq+uBNrrOGONQyyhkc+nE3+fThl89LuMlYYhmr3NLVnm6pqaZakmN84+azGbrtReXgnXtk42NX6hJiTHU4nzxf0cUNB38Awa5knN8I5Us57DhW/4AOI5hfcmNOZxh8s7gfwsHEAN/9wcT+ER41DuDkHjF9whTiKqraC8xbCmHd3qt1JqbokifdbbRtB/HKk35duNjm830n/OXI8OjVsFOh/i0PHRiH+dI8d8/C8fhjzfp8E+r4xibMxh4ibkf2wD7IfGoPs9zsv3Azl5T5QXjYGygYcDb6XkH6QdOxyE4vTpZgvxb5KtjY7iKXpT/mv2fyj/+HQP4d19Uh/bQ7ST/p8btYcnM/9SK5T/icBvJ7/N62X/wdQSwcIz7rzQucIAAD9SwAAUEsBAhQAFAAICAgAFXooRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAVeihEz7rzQucIAAD9SwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAH4JAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | <ggb_applet width="649" height="515" version="4.2" ggbBase64="UEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vzdctu2Er5OnwLDi3MVSQT/ROVI6URqfpw4beY4p9M5NxmIhChEFMmSlH8yfZy+SV/sLACSIiVKlmRZodxqbIMgFljg28XuR9B2/8fbuY+uaZywMBgouK0qiAZO6LLAGyiLdNKylR9f/tD3aOjRcUzQJIznJB0oRltTlv2g1rZU3pm5A0WdTDSHqnbLwdhtGbo+aY1N3W1NyMRwbU3Hlu0oCN0m7EUQ/kzmNImIQ6+cKZ2Ty9AhqRhzmqbRi07n5uamnWtvh7HX8bxx+zZxFQQzD5KBkl28gOEqnW50Ia6pKu789vFSDt9iQZKSwKEK4qtasJc/POvfsMANb9ANc9PpQLHMroKmlHlTWKalwpo6XCiCtUbUSdk1TaBrqSrWnM4jRYiRgLc/k1fIL5ajIJddM5fGgE9bVw0DG6oqSwWFMaNBmkniTGMnH6t/zeiNHJRfCX3QKQ1Df0z4eOiPP5Cmaip6zgssCw0Ky5JNqryn6rLQZGHIwpQyhuxuSFFDyhhSxtDB2CxhY58OlAnxE8CPBZMYbFfUk/TOp2I+2Y3l2vFzWFPCvoGwzgGVgMN9VX3OvwHl50aOdGmRuKQ1jRdblcr2ks5co2X0dteoPWideq5Tq1ulZtbrtB+Gba4TmyWdoEp8ie91XK0tKiWQR9aobwN2VeNGU+6h0DJOvURD7XWPvsguBr/pahuVdtVT4Nrv5BGonwUdlEy5bLYpUzpPeBjSe8js8WiCkQkhx+pC8DAR7kHR1RAEGYRNZJhQxTayeNlFehcaDKQjG3E5rCMRc0wbfhhdMZiFTBiM3+1CqEMYFBnI1BEWocpAEKCQCHcQ+jQdJEwTmdCJq8caH0K3kGFBTbeRAXPkka6LQVCHjlAH9RrSMdJ5Z9xFmoUsPh42eAS1bD51GFJDlooszAeEYAmBUgZJkLeRzlcD2yoKE1agO6V+lIMkcGRBtEgr2DlzN79Mw6iwoZB2Q2c2LLDOWihJ0rIYpIllKpJpo5KpnvV9MqY+5PMr7ggIXROfRyqhYRIGKcqdQJP3vJhEU+YkVzRNoVeCvpJrcklSevsGpJNct1AtEmifLhyfuYwEv4KX8CH4gKjIpzz+5vnU0LtSixOGsXt1l4DroNv/0TiEoKkBgyh/IJzeySbdxtUmQDpxCHd6c6UTBJq7DU2WVE2vi6WRW1osCHkxK2zBry+SYei7RXMUsiAdkShdxIIcwexivqhXgedTga1IH0AznNk4vL2SoOpyrM93EdRUOYGxNwr9MEawJTXTBIGsHMtSyPCZFVKqkFGFhJpbiblFO+5pQkKUY1kKKTC7nFq2UpyvEqu5GpZIzqZU3Uw4DWcti4Cll3klZc4sWyqWHX5ezMfgbxlu1THxscbsd1ZcrD+jcUB96UgB2HIRLhLp2YV3PusvEvqJpNNXgfsf6sGe/ER4XExhaCm6nLJLHTaHjvJ+Bh7hhv0vTFXedakX03yJvuCjElrRqpbdeu22GOpNHM4vguvP4DUrU+138vX0EydmEXdONIZAPaNL/3NZQiDMu+V+sPgEVuHwiANAphxEBZFFOg1jQTlh2wLBQO//+jMIaAyBEtgm37E+nQPhRKlwS+HZhXleCR7L7YDC8VeII0XikO1L1KC51kWFMxM/mhLOdTMIfHIHEyiDIsb7GLqrUIElxHogNkTSJyJKpTvJ+cJFBMOJXVgyt8A+QbcDpaXxR5E7/lwC5Tf5XCNZPF8q35qVMCjvrlgNnE6idA9ew/PHC58QrtH5w6VmcGlHgssJ53MSuCgQrO1T6N95YaAs+QJR+a5EBHNnQ0TjIEqEFmneDnHRh8SDpZgjxQgU+kAZS4WZmhr7SIW5BYqhqhkkBVIwgwfSRKS5NEto4uIdc10qKE9nu3FLcJati01d2NfEWYpbmhfvY97NPphQj9eKiTj3eOH+E93TD9e9Sc+8qYW1YrADwAef8LnvXgQ80VGRGtZT44zSiHOSX4LPMQkSfqpTzYm7Q0maA2Ue9ls4w/K8kBw3B8kig7byIGc0GspqjvlpHcgqBT2DJKOfMCe/Pi1ev0wmCU0F8bBkItVOhSY+AZpvnoD3mStJ6RQU5yfJXV5L7vJmE8XRpNhEirmS4tCDKI52HIpTtW5jOM7kPj88YT7J95+ak5xeo9PJKpRug6AsUvN5ZOZVKGmToMSrLAfjRoNZTTRvn0CiyZ3ZPEFifveE8FLb9iMk5ktw+pWs/Fam23dr6djbnnL5/imA9Q7c9NWD7yPsePFrC+U8ZLeNw/c7/T2QXRJ5fs3mkc8clu7jlBdPwCnzMGo9ClusccoL6ZRv15xyuodTTpvilDl8+cNJq/uQJLSrU1ZB/sjiOIzrDx29NZhf/YtEYfLv+0h35bVC1uX7evsSdGv5fF354Efw4Fpwh5vAHe4P7rBh4GrtXvVjHfUsYwd0R5vQHe2P7qhh6BrLB4Dqxzjd64gMEvlSoqhoFXxrX1CUOzrljqSo8FcWu1mp/sVFyVxP9dne2c0lH3m+Zae027aNu7aBe10IopqpvW5lp3stfYOfntfpPGkc5Lg+yuJ6uFtYPSu8x43Du1UXcBt8ELMLwyuH4+kmnncw29tkwkd84798uWDL3WA+iLIc64XBLoRwuy2Gh9pi+N1sscOB8Ckp4XZ8R4fiO2oivqUXON+ZI9YwxRq+uBNrrOGONQyyhkc+nE3+fThl89LuMlYYhmr3NLVnm6pqaZakmN84+azGbrtReXgnXtk42NX6hJiTHU4nzxf0cUNB38Awa5knN8I5Us57DhW/4AOI5hfcmNOZxh8s7gfwsHEAN/9wcT+ER41DuDkHjF9whTiKqraC8xbCmHd3qt1JqbokifdbbRtB/HKk35duNjm830n/OXI8OjVsFOh/i0PHRiH+dI8d8/C8fhjzfp8E+r4xibMxh4ibkf2wD7IfGoPs9zsv3Azl5T5QXjYGygYcDb6XkH6QdOxyE4vTpZgvxb5KtjY7iKXpT/mv2fyj/+HQP4d19Uh/bQ7ST/p8btYcnM/9SK5T/icBvJ7/N62X/wdQSwcIz7rzQucIAAD9SwAAUEsBAhQAFAAICAgAFXooRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAVeihEz7rzQucIAAD9SwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAH4JAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | ||
| + | mein Lösungsvorschlag--[[Benutzer:Werzdavid|Werzdavid]] ([[Benutzer Diskussion:Werzdavid|Diskussion]]) 18:54, 22. Jan. 2021 (CET)<br /> | ||
| + | '''Vorgehen''': | ||
| + | * Überlegung: einmal schräg und einmal senkrecht zu spiegeln scheint nach Skizze sinnvoll. | ||
| + | * weitere Überlegung: den Punkt <math>B</math> bei der ersten Spiegelung direkt auf <math>B''</math> spiegeln und die zweite Spiegelachse durch den Punkt <math>B''</math> laufen lassen. | ||
| + | * Die Mittelsenkrechte zwischen <math>B</math> und <math>B''</math> einzeichnen und alle Punkte des Dreiecks <math>\overline{ABC}</math> spiegeln. | ||
| + | * Die zweite Spiegelachse ist die Mittelsenkrechte von <math>\overline{CC''}</math><br /> | ||
| + | {|class="wikitable" | ||
| + | |- | ||
| + | | Bemerkung: Die Punkte sind in meiner Lösung falsch beschriftet ;) | ||
| + | |} | ||
| + | |||
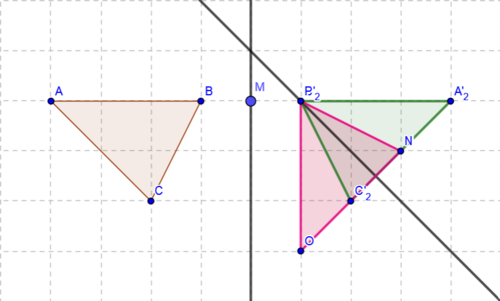
| + | [[Datei:Übung10.1.png|500px|Aufgabe zur Übung 10.1]] | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 22. Januar 2021, 18:54 Uhr
Das Dreieck 
wurde durch die Nacheinanderausführung zweier verschiedener Geradenspiegelungen auf das Dreieck 
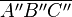abgebildet. Konstruieren Sie die beiden Spiegelgeraden.
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren
mein Lösungsvorschlag--Werzdavid (Diskussion) 18:54, 22. Jan. 2021 (CET)
Vorgehen:
- Überlegung: einmal schräg und einmal senkrecht zu spiegeln scheint nach Skizze sinnvoll.
- weitere Überlegung: den Punkt
bei der ersten Spiegelung direkt auf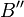 
spiegeln und die zweite Spiegelachse durch den Punkt 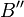laufen lassen.
- Die Mittelsenkrechte zwischen und 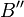einzeichnen und alle Punkte des Dreiecks spiegeln.
- Die zweite Spiegelachse ist die Mittelsenkrechte von
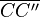
| Bemerkung: Die Punkte sind in meiner Lösung falsch beschriftet ;) |
