Lösung von Aufgabe 5.3 P (SoSe 22): Unterschied zwischen den Versionen
Kwd077 (Diskussion | Beiträge) |
Kwd077 (Diskussion | Beiträge) |
||
| Zeile 18: | Zeile 18: | ||
Beachte: der Drache ist keine Teilmenge des Quadrats, wie auch das Rechteck, somit steht nur das Quadrat mit dem Drachen in Relation nicht aber andersrum. Zudem fehlt noch ein Viereckspaar in deiner Relation.--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 15:11, 19. Mai 2022 (CEST) | Beachte: der Drache ist keine Teilmenge des Quadrats, wie auch das Rechteck, somit steht nur das Quadrat mit dem Drachen in Relation nicht aber andersrum. Zudem fehlt noch ein Viereckspaar in deiner Relation.--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 15:11, 19. Mai 2022 (CEST) | ||
zu c) Relation : (D,D), (Q,Q), (R,R), (Q,D), (D,R)--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 21:01, 20. Mai 2022 (CEST) | zu c) Relation : (D,D), (Q,Q), (R,R), (Q,D), (D,R)--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 21:01, 20. Mai 2022 (CEST) | ||
| + | (D,R) war falsch, ich wollte (Q,R)--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 21:01, 20. Mai 2022 (CEST) | ||
Aktuelle Version vom 20. Mai 2022, 20:01 Uhr
a) Geben Sie die Menge 
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge 
.
c) Wir definineren eine Relation 
mit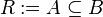 
. Bestimmen Sie die Relation auf .
d) Untersuchen Sie die Relation auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
a) Menge aller konvexen Drachenvierecke: Menge aller Drachen D, Menge aller Rauten R und Menge aller Quadrate Q b)MxM= {(D,D), (D,R), (D,Q), (R,R), (R,Q), (R,D), (Q,Q), (Q,R), (Q,D)} c) Relation: (D,D), (Q,Q), (R,R), (D,Q), (R,Q) d) reflexiv ja, da in der Relation alle Elemente A in Relation zu sich selbst stehen
symmetrisch ja, da in der Relation A in Relation zu B steht transitiv: würde sagen ja--Kwd077 (Diskussion) 13:45, 16. Mai 2022 (CEST)
Beachte: der Drache ist keine Teilmenge des Quadrats, wie auch das Rechteck, somit steht nur das Quadrat mit dem Drachen in Relation nicht aber andersrum. Zudem fehlt noch ein Viereckspaar in deiner Relation.--Matze2000 (Diskussion) 15:11, 19. Mai 2022 (CEST) zu c) Relation : (D,D), (Q,Q), (R,R), (Q,D), (D,R)--Kwd077 (Diskussion) 21:01, 20. Mai 2022 (CEST) (D,R) war falsch, ich wollte (Q,R)--Kwd077 (Diskussion) 21:01, 20. Mai 2022 (CEST)
