Lösung von Aufgabe 5.3 P (WS 23 24): Unterschied zwischen den Versionen
End007 (Diskussion | Beiträge) |
|||
| Zeile 8: | Zeile 8: | ||
zu Aufgabe c habe ich eine Frage: was ist A und was ist B das ist hier nicht definiert oder? Es steht ja nur da dass die Relation R als "A ist die Teilmenge von B" definiert ist.--[[Benutzer:End007|End007]] ([[Benutzer Diskussion:End007|Diskussion]]) 15:17, 20. Nov. 2023 (CET) | zu Aufgabe c habe ich eine Frage: was ist A und was ist B das ist hier nicht definiert oder? Es steht ja nur da dass die Relation R als "A ist die Teilmenge von B" definiert ist.--[[Benutzer:End007|End007]] ([[Benutzer Diskussion:End007|Diskussion]]) 15:17, 20. Nov. 2023 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
| + | |||
| + | Genau du hast die Relation schon richtig verstanden :). Wenn du die Relation jetzt auf das kartesische Produkt M x M, dass du in Aufgabe b) schon richtig gebildet hast, anwendest, bleiben nur Paare aus M x M in der Relation, bei denen die erste Menge (A) Teilmenge der zweiten Menge (B). | ||
| + | |||
| + | Also z. B. auch das Paar (Q,D), da die Menge aller Quadrate eine Teilmenge der Menge aller Drachenvierecke ist.--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 16:17, 20. Nov. 2023 (CET) | ||
Version vom 20. November 2023, 16:17 Uhr
a) Geben Sie die Menge  aller konvexer Drachenvierecke an.
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge  .
.
c) Wir definineren eine Relation  mit
mit 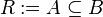 . Bestimmen Sie die Relation
. Bestimmen Sie die Relation  auf
auf  .
.
d) Untersuchen Sie die Relation  auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
Mein Vorschlag: a) M= {Drache, Raute, Quadrat} b) MxM= {(D,D); (D,R); (D,Q); (R,R); (R,D); (R,Q); (Q,Q); (Q,R); (Q,D)}--End007 (Diskussion) 15:17, 20. Nov. 2023 (CET)
zu Aufgabe c habe ich eine Frage: was ist A und was ist B das ist hier nicht definiert oder? Es steht ja nur da dass die Relation R als "A ist die Teilmenge von B" definiert ist.--End007 (Diskussion) 15:17, 20. Nov. 2023 (CET)
Genau du hast die Relation schon richtig verstanden :). Wenn du die Relation jetzt auf das kartesische Produkt M x M, dass du in Aufgabe b) schon richtig gebildet hast, anwendest, bleiben nur Paare aus M x M in der Relation, bei denen die erste Menge (A) Teilmenge der zweiten Menge (B).
Also z. B. auch das Paar (Q,D), da die Menge aller Quadrate eine Teilmenge der Menge aller Drachenvierecke ist.--Matze2000 (Diskussion) 16:17, 20. Nov. 2023 (CET)

