Lösung von Aufgabe 4.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 4: | Zeile 4: | ||
stimmt<br /> | stimmt<br /> | ||
--> Ich würde sagen stimmt nicht, weil bei der Relation Schnittpunkt die Gerade a zu sich selbst doch keinen Schnittpunkt haben kann?! | --> Ich würde sagen stimmt nicht, weil bei der Relation Schnittpunkt die Gerade a zu sich selbst doch keinen Schnittpunkt haben kann?! | ||
| + | |||
<u>Symmetrie:</u> aRb bRa<br /> | <u>Symmetrie:</u> aRb bRa<br /> | ||
stimmt<br /> | stimmt<br /> | ||
--> Stimmt! Wenn a zu b einen Schnittpunkt hat, dann hat auch b zu a einen Schnittpunkt! | --> Stimmt! Wenn a zu b einen Schnittpunkt hat, dann hat auch b zu a einen Schnittpunkt! | ||
| + | |||
<u>Transitivität:</u> aRb bRc draus folgt aRc<br /> | <u>Transitivität:</u> aRb bRc draus folgt aRc<br /> | ||
stimmt nicht--[[Benutzer:Engel82|Engel82]] 12:47, 4. Nov. 2010 (UTC) | stimmt nicht--[[Benutzer:Engel82|Engel82]] 12:47, 4. Nov. 2010 (UTC) | ||
--> Würde auch sagen stimmt nicht! a und c können parallel zueinander sein und beide von b geschnitten werden! | --> Würde auch sagen stimmt nicht! a und c können parallel zueinander sein und beide von b geschnitten werden! | ||
Version vom 6. November 2010, 15:26 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
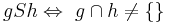
Reflexivität: aRa
stimmt
--> Ich würde sagen stimmt nicht, weil bei der Relation Schnittpunkt die Gerade a zu sich selbst doch keinen Schnittpunkt haben kann?!
Symmetrie: aRb bRa
stimmt
--> Stimmt! Wenn a zu b einen Schnittpunkt hat, dann hat auch b zu a einen Schnittpunkt!
Transitivität: aRb bRc draus folgt aRc
stimmt nicht--Engel82 12:47, 4. Nov. 2010 (UTC)
--> Würde auch sagen stimmt nicht! a und c können parallel zueinander sein und beide von b geschnitten werden!

