Übungsaufgaben 5 EG WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Aufgabe 1) |
|||
| Zeile 2: | Zeile 2: | ||
Es seien <math>\ a, b, c</math> drei paarweise nicht identische Geraden der Ebene, die alle drei den Punkt <math>\ Z</math> gemeinsam haben. Man beweise <math>\ S_c \circ S_b \circ S_a</math> ist eine Geradenspiegelung. | Es seien <math>\ a, b, c</math> drei paarweise nicht identische Geraden der Ebene, die alle drei den Punkt <math>\ Z</math> gemeinsam haben. Man beweise <math>\ S_c \circ S_b \circ S_a</math> ist eine Geradenspiegelung. | ||
[[Aufgabe 1 Lösung (Skizze)]] | [[Aufgabe 1 Lösung (Skizze)]] | ||
| + | |||
| + | |||
| + | [[Aufgabe 1 Lösungsversuch]] | ||
Aktuelle Version vom 6. Dezember 2010, 16:43 Uhr
Aufgabe 1
Es seien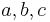 
drei paarweise nicht identische Geraden der Ebene, die alle drei den Punkt 
gemeinsam haben. Man beweise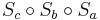 
ist eine Geradenspiegelung.
Aufgabe 1 Lösung (Skizze)
