Lösung von Aufg. 8.2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right|</math> und <math>\overline{AB^{*}} \subset \overline{AB}</math>.<br /> | Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right|</math> und <math>\overline{AB^{*}} \subset \overline{AB}</math>.<br /> | ||
| − | Vor: <math>\overline{AB}</math> | + | <u>Vor</u>: <math>\overline{AB}</math> <br /> |
| − | Beh: Es existiert <math>\overline{AB*}</math>, <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right| </math>,<math>\overline{AB^{*}} \subset \overline{AB}</math>.<br /> | + | <u>Beh:</u> Es existiert <math>\overline{AB*}</math>, <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right| </math>,<math>\overline{AB^{*}} \subset \overline{AB}</math>.<br /> |
| + | |||
| + | 1)<math>\overline{AB}</math>___________________laut Vor<br /> | ||
| − | |||
2) es existiert ein Strahl AB+_________________Def. Strahl<br /> | 2) es existiert ein Strahl AB+_________________Def. Strahl<br /> | ||
| + | |||
3) es existiert genau ein Punkt B* auf_______________________Axiom vom Lineal<br /> | 3) es existiert genau ein Punkt B* auf_______________________Axiom vom Lineal<br /> | ||
dem Strahl AB+ für den gilt: | dem Strahl AB+ für den gilt: | ||
<math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right|</math><br /> | <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right|</math><br /> | ||
| + | |||
4) <math>\pi</math> ist größer als 1. daraus folgt_____________________Rechnen in R<br /> | 4) <math>\pi</math> ist größer als 1. daraus folgt_____________________Rechnen in R<br /> | ||
<math \frac{1}{\pi}></math> kleiner als 1 ist daraus<br /> | <math \frac{1}{\pi}></math> kleiner als 1 ist daraus<br /> | ||
folgt wiederum <math>\left| AB^{*} \right|</math> kleiner als <math>\left| AB \right|</math><br /> | folgt wiederum <math>\left| AB^{*} \right|</math> kleiner als <math>\left| AB \right|</math><br /> | ||
| − | 5) Zw(A,B*,B)____________________________4) | + | |
| − | 6)<math>\left| AB^{*} \right|</math> + <math>\left| BB^{*} \right|</math>= <math>\left| AB\right|</math>_________Def. Zw 5) | + | 5) Zw(A,B*,B)____________________________4)<br /> |
| − | 7)<math>\overline{AB}</math>:=(P\ Zw(A,P,B*))<math>\cup AB*</math> | + | |
| + | 6)<math>\left| AB^{*} \right|</math> + <math>\left| BB^{*} \right|</math>= <math>\left| AB\right|</math>_________Def. Zw 5)<br /> | ||
| + | |||
| + | 7)<math>\overline{AB}</math>:=(P\ Zw(A,P,B*))<math>\cup AB*</math>________________Def. Strecke<br /> | ||
| + | |||
| + | 8)<math>\overline{AB}</math>:= <math>\overline{AB*}</math> <math>\cup</math>(P\ Zw(B*,P,B)<math>\cup B</math> _____Def. Strecke<br /> | ||
| + | |||
| + | 9)<math>\overline{AB^{*}} \subset \overline{AB}</math>.<br />--[[Benutzer:Engel82|Engel82]] 17:55, 3. Dez. 2010 (UTC) | ||
Version vom 3. Dezember 2010, 18:55 Uhr
Beweisen Sie: Zu jeder Strecke 
existiert genau eine Strecke 
mit 
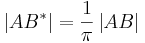und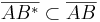 
.
Vor:
Beh: Es existiert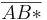 
, ,.
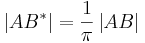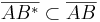1)___________________laut Vor
2) es existiert ein Strahl AB+_________________Def. Strahl
3) es existiert genau ein Punkt B* auf_______________________Axiom vom Lineal
dem Strahl AB+ für den gilt:
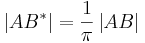
4) 
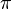ist größer als 1. daraus folgt_____________________Rechnen in R
kleiner als 1 ist daraus
folgt wiederum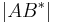 
kleiner als 
5) Zw(A,B*,B)____________________________4)
6) + 
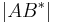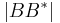= _________Def. Zw 5)
7):=(P\ Zw(A,P,B*))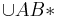
________________Def. Strecke
8):= 
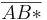
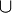(P\ Zw(B*,P,B)
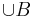_____Def. Strecke
9).
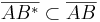--Engel82 17:55, 3. Dez. 2010 (UTC)
