Der schwache Außenwinkelsatz (WS10/11): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: ===== Definition VIII.1 (Außenwinkel eines Dreiecks): ===== Gegeben sei ein Dreieck <math>\overline {ABC}</math>. Alle Nebenwinkel der Innenwinkel des Dreiecks <math>...) |
|||
| Zeile 46: | Zeile 46: | ||
Übungsaufgabe | Übungsaufgabe | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 13. Januar 2011, 09:56 Uhr
Inhaltsverzeichnis |
Definition VIII.1 (Außenwinkel eines Dreiecks):
Gegeben sei ein Dreieck 
. Alle Nebenwinkel der Innenwinkel des Dreiecks heißen Außenwinkel des Dreiecks .
schwacher Außenwinkelsatz?
In der Vorlesung wurde angedeutet, dass es im Rahmen der absoluten Geometrie nicht möglich ist, den Satz über die Summe der Größen der Innenwinkel eines Dreiecks zu beweisen. Wenn es richtig ist, was in der Vorlesung gesagt wurde, dann dürfte es in der absoluten Geometrie auch nicht möglich sein, den sogenannten starken Außenwinkelsatz zu beweisen. Die folgende Applikation demonstriert den starken Außenwinkelsatz:
Egal, wie wir unser Dreieck wählen, es gilt immer 
.
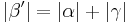Allgemeiner formuliert:
Für jedes Dreieck gilt: Die Größe eines jeden Außenwinkels ist immer gleich der Summe der Größen der beiden Innenwinkel des Dreiecks, die zu dem jeweiligen Außenwinkel keine Nebenwinkel sind.
Wie bereits erwähnt, gilt der starke Außenwinkelsatz im Rahmen der absoluten Geometrie nicht. Es gilt jedoch der sogenannte schwache Außenwinkelsatz. Dieser ist selbstverständlich im starken Außenwinkelsatz aufgehoben.
Satz VIII.1: (schwacher Außenwinkelsatz)
- Die Größe eines jeden Außenwinkels eines Dreiecks ist jeweils größer als die Größe eines jeden Innenwinkels dieses Dreiecks, der kein Nebenwinkel zu dem gewählten Außenwinkel des Dreiecks ist.
Für den Beweis des schwachen Außenwinkelsatzes formulieren wir zunächst ein Lemma.
Lemma 2
- Wenn ein Punkt
im Inneren des Winkels 
liegt, dann liegt der gesamte Strahl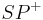 
im Inneren des Winkels .
- Wenn ein Punkt
Hinsichtlich des Beweises von Lemma 2 verweisen wir auf das alte Skript (Geschichten aus dem Inneren).
Beweis von Satz VIII.1
Hilfskonstruktion
Der letztendliche Beweis
Es bleibt zu zeigen: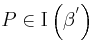 
, wobei wir in diesem Fall das offene Innere von 
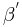meinen.
Ziehen Sie an dem Punkt und versuchen Sie, den Beweis nachzuvollziehen.
Unmittelbare Folgerungen aus dem schwachen Außenwinkelsatz
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Übungsaufgabe
Korollar 2 zum schwachen Außenwinkelsatz
- Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Übungsaufgabe
