Lösung von Aufg. 13.3: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 5: Zeile 5:
  
 
1)<math>\angle ASP</math> <math>\cong</math><math>\angle PSB</math>__________________Vor<br />
 
1)<math>\angle ASP</math> <math>\cong</math><math>\angle PSB</math>__________________Vor<br />
−
2)Lote werden durch P auf dei jeweiligen Schenkel des Winkels________________Existenz und Eindeutigkeit des Lotes<br />
+
2)Lote werden durch P auf die jeweiligen Schenkel des Winkels________________Existenz und Eindeutigkeit des Lotes<br />
 
<math>\angle ASB</math> gefällt<br />
 
<math>\angle ASB</math> gefällt<br />
 
3)|<math>\angle {SAP}</math>| =|<math>\angle {SBP}</math>| =90________________2)<br />
 
3)|<math>\angle {SAP}</math>| =|<math>\angle {SBP}</math>| =90________________2)<br />

Version vom 25. Januar 2011, 18:24 Uhr

Man beweise: Ein Punkt \ P gehört genau dann zur Winkelhalbierenden des Winkels \ \alpha, wenn er zu den Schenkeln von \ \alpha jeweils denselben Abstand hat.

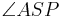
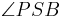
Vor: P gehört zur Winkelhalbierenden w, \angle ASP \cong\angle PSB
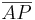
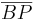
Beh: \overline {AP} \cong\overline {BP}

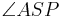
1)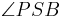\angle ASP \cong\angle PSB__________________Vor
2)Lote werden durch P auf die jeweiligen Schenkel des Winkels________________Existenz und Eindeutigkeit des Lotes
\angle ASB gefällt
3)|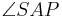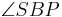\angle {SAP}| =|\angle {SBP}| =90________________2)
4)\overline {SP}= \overline {SP}___________________trivial
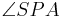
5)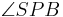\angle SPA\cong\angle SPB__________________1), 2) und Innenwinkelsumme im Dreieck
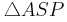
6)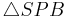\triangle {ASP} \cong\triangle {SPB}______________WSW,1), 4),5)
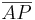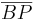7) \overline {AP}= \overline {BP}______________________6)--Engel82 17:22, 25. Jan. 2011 (UTC)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._13.3&oldid=6163“