Lösung von Aufgabe 3.5 (SoSe11): Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
|- | |- | ||
| 1) <math>\overline{AX}</math> ist kongruent zu <math>\overline{BX}</math><br /> 2) <math>\overline{MX}</math> ist kongruent zu <math>\overline{MX}</math><br /> 3) <math>\overline{AM}</math> ist kongruent zu <math>\overline{BM}</math><br /> 4) Dreieck <math>\overline{AMX}</math> ist kongruent zu Dreieck <math>\overline{BMX}</math><br /> 5) <math>\angle (M,A,X)</math> ist kongruent zu <math>\angle (M,B,X)</math> || Voraussetzung<br />trivial<br />Voraussetzung, Def. Mittelpunkt<br />Kongruenzsatz SSS, 1-3<br />4 | | 1) <math>\overline{AX}</math> ist kongruent zu <math>\overline{BX}</math><br /> 2) <math>\overline{MX}</math> ist kongruent zu <math>\overline{MX}</math><br /> 3) <math>\overline{AM}</math> ist kongruent zu <math>\overline{BM}</math><br /> 4) Dreieck <math>\overline{AMX}</math> ist kongruent zu Dreieck <math>\overline{BMX}</math><br /> 5) <math>\angle (M,A,X)</math> ist kongruent zu <math>\angle (M,B,X)</math> || Voraussetzung<br />trivial<br />Voraussetzung, Def. Mittelpunkt<br />Kongruenzsatz SSS, 1-3<br />4 | ||
| − | |}<br />→Jeder Punkt X mit dem gleichen Abstand zu A und B liegt auf der Mittelsenkrechten g--[[Benutzer:Matthias|Matthias]] 19:16, 27. Apr. 2011 (CEST) | + | |}<br />→Jeder Punkt X mit dem gleichen Abstand zu A und B liegt auf der Mittelsenkrechten g--[[Benutzer:Matthias|Matthias]] 19:16, 27. Apr. 2011 (CEST)<br /> |
| + | <span style="color:navy"> Wozu zeigst du Matthias in Schritt 2, dass <math>\angle (M,A,X)</math> <math>\cong</math> <math>\angle (M,B,X)</math> ist(Behauptung 2) ?<br /> | ||
| + | <span style="color:navy">Die benannten Winkel entsprechen alpha und betha bei ülicher Bezeichung im Dreieck. Oder meinst du vllt andere Winkel? --[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:16, 30. Apr. 2011 (CEST)<br /> | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 30. April 2011, 18:16 Uhr
Der Begriff Mittelsenkrechte sei folgendermaßen definiert:
Die Mittelsenkrechte einer Strecke  ist die Gerade g, die durch den Mittelpunkt von
ist die Gerade g, die durch den Mittelpunkt von  verläuft und zu dieser Strecke
verläuft und zu dieser Strecke  senkrecht steht.
senkrecht steht.
Beweisen Sie folgenden Satz:
Die Mittelsenkrechte m einer beliebigen Strecke  ist die Menge aller Punkte P, die von A und B denselben Abstand haben:
ist die Menge aller Punkte P, die von A und B denselben Abstand haben:
(Beachten Sie, dass auch dieser Beweis wieder aus zwei Teilen besteht analog zur Aufgabe 3.4).
Lösung: Schritt 1 Voraussetzung:  mit Mittelpunkt M, Mittelsenkrechte m und ein beliebiger Punkt P, wobei P ԑ m
mit Mittelpunkt M, Mittelsenkrechte m und ein beliebiger Punkt P, wobei P ԑ m
Behauptung: zu zeigen: 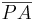 ist kongruent zu
ist kongruent zu 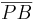
| Beweisschritt | Behauptung |
1) 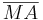 ist kongruent zu ist kongruent zu  2) 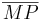 ist kongruent zu ist kongruent zu 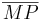 3) 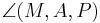 ist kongruent zu ist kongruent zu 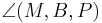 4) Dreieck 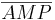 ist kongruent zu Dreieck ist kongruent zu Dreieck 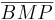 5) 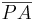 ist kongruent zu ist kongruent zu 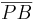 |
Voraussetzung, Def. Mittelpunkt trivial Voraussetzung, Definition Mittelsenkrechte Kongruenzsatz SWS, 1-3 5 |
→Jeder Punkt P auf der Geraden g hat den gleichen Abstand zu A und B
Schritt 2: Voraussetzung:  mit Mittelpunkt M, Mittelsenkrechte m und ein beliebiger Punkt X, für den gilt
mit Mittelpunkt M, Mittelsenkrechte m und ein beliebiger Punkt X, für den gilt 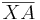 ist kongruent zu
ist kongruent zu 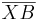
Behauptung: zu zeigen: 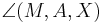 ist kongruent zu
ist kongruent zu 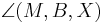
| Beweisschritt | Behauptung |
1) 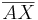 ist kongruent zu ist kongruent zu 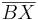 2) 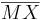 ist kongruent zu ist kongruent zu 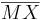 3) 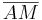 ist kongruent zu ist kongruent zu 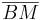 4) Dreieck 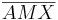 ist kongruent zu Dreieck ist kongruent zu Dreieck 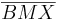 5) 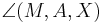 ist kongruent zu ist kongruent zu 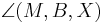 |
Voraussetzung trivial Voraussetzung, Def. Mittelpunkt Kongruenzsatz SSS, 1-3 4 |
→Jeder Punkt X mit dem gleichen Abstand zu A und B liegt auf der Mittelsenkrechten g--Matthias 19:16, 27. Apr. 2011 (CEST)
Wozu zeigst du Matthias in Schritt 2, dass 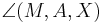

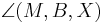 ist(Behauptung 2) ?
ist(Behauptung 2) ?
Die benannten Winkel entsprechen alpha und betha bei ülicher Bezeichung im Dreieck. Oder meinst du vllt andere Winkel? --Tutorin Anne 19:16, 30. Apr. 2011 (CEST)

