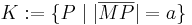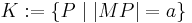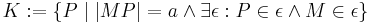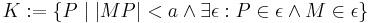Aus den Übungen mit dem Classroompresenter (SoSe 2011): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 01) |
*m.g.* (Diskussion | Beiträge) (→Übung vom 13.05.2011) |
||
| Zeile 15: | Zeile 15: | ||
Was für ein geometrisches Objekt wird durch die folgende Menge definiert? | Was für ein geometrisches Objekt wird durch die folgende Menge definiert? | ||
| − | <math>M := \lbrace Q \mid \overline{AQ} \cong \overline{QB} \rbrace</math> | + | <math>M := \lbrace Q \mid \overline{AQ} \cong \overline{QB} \rbrace</math><br /><br /> |
| + | Nicht korrekte Lösung: <br /> | ||
| + | <iframe src="http://www.ph-heidelberg.de/wp/gieding/Uebungen/Uebung_01/Neuer%20Ordner/Student%20Submissions_008.png" width="720" height="540" frameborder="2"></iframe><br /> | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 19. Mai 2011, 12:34 Uhr
Übung vom 13.05.2011
Aufgabe 01
Ein Kreis ist die Menge aller Punkte einer Ebene 
, die zu einem gegebenen Punkt dieser Ebene ein und denselben Abstand haben.
Es seien 
ein beliebiger Punkt des Raumes und 
eine positive reelle Zahl. Im Folgenden wird jeweils eine Menge von Punkten definiert, die sich auf und beziehen. Welche der Mengen ist ein Kreis?
Korrekte Lösung aus der Übung:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Aufgabe 02
Wir setzen ebene Geometrie voraus.
Es seien 
und 
zwei verschiedene Punkte der Ebene.
Was für ein geometrisches Objekt wird durch die folgende Menge definiert?
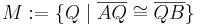
Nicht korrekte Lösung:
[ www.ph-heidelberg.de is not an authorized iframe site ]
