Probeklausur (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→e) |
*m.g.* (Diskussion | Beiträge) (→f) |
||
| Zeile 19: | Zeile 19: | ||
<math>\varepsilon \subset \mathbb{P}</math> sei eine Ebene. Gegeben sei ferner <math>\ Q</math> mit <math>Q \in \mathbb{P} \land Q \not \in \varepsilon</math>. Definieren Sie die Begriffe Halbraum <math>\varepsilon Q^+</math> und <math>\varepsilon Q^-</math>. | <math>\varepsilon \subset \mathbb{P}</math> sei eine Ebene. Gegeben sei ferner <math>\ Q</math> mit <math>Q \in \mathbb{P} \land Q \not \in \varepsilon</math>. Definieren Sie die Begriffe Halbraum <math>\varepsilon Q^+</math> und <math>\varepsilon Q^-</math>. | ||
====f==== | ====f==== | ||
| − | + | Definieren Sie den Begriff regelmäßiges Sechseck. Der Begriff n-Eck sei bereits | |
| − | + | definiert. | |
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Version vom 24. Juni 2011, 12:18 Uhr
Inhaltsverzeichnis |
Die Klausur als PDF
Die Klausuraufgaben zum Diskutieren
Aufgabe 1
a
Definieren Sie den Begriff offene Strecke 
b
Definieren Sie, was man unter dem Kreis 
mit dem Radius 
und dem Mittelpunkt
versteht.
c
Definieren Sie den Begriff Inneres eines Kreises.
d
Was ist an der folgenden Definition nicht korrekt?
Definition (gleichschenkliges Dreieck):
- Wenn ein Dreieck zueinander kongruente Basiswinkel hat, so ist es gleichschenklig.
e
Unter dem Raum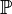 
versteht man die Menge aller Punkte. Die Punktmenge
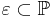sei eine Ebene. Gegeben sei ferner 
mit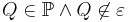 
. Definieren Sie die Begriffe Halbraum 
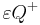und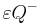 
.
f
Definieren Sie den Begriff regelmäßiges Sechseck. Der Begriff n-Eck sei bereits definiert.
