Lösung von Aufg. 12.9 SS11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Es seien <math>\overline{ABC}</math> ein gleichseitiges Dreieck und <math>r</math> eine positive reelle Zahl, die kleiner als die Seitenlänge von <math>\overline…“) |
|||
| Zeile 1: | Zeile 1: | ||
Es seien <math>\overline{ABC}</math> ein gleichseitiges Dreieck und <math>r</math> eine positive reelle Zahl, die kleiner als die Seitenlänge von <math>\overline{ABC}</math> ist. Ferner seien die Punkte <math> E \in \overline{AB}, F \in \overline{BC}, G \in \overline{CA} </math> mit <math>\ |AE|=|BF|=|CG|=r</math> gegeben. Man beweise: <math>\overline{EFH}</math> ist ein gleichseitiges Dreieck. | Es seien <math>\overline{ABC}</math> ein gleichseitiges Dreieck und <math>r</math> eine positive reelle Zahl, die kleiner als die Seitenlänge von <math>\overline{ABC}</math> ist. Ferner seien die Punkte <math> E \in \overline{AB}, F \in \overline{BC}, G \in \overline{CA} </math> mit <math>\ |AE|=|BF|=|CG|=r</math> gegeben. Man beweise: <math>\overline{EFH}</math> ist ein gleichseitiges Dreieck. | ||
| + | <br><br><br> | ||
| + | |||
| + | Auch hier wäre die Definiont des gleichseitigen Dreiecks gefragt. | ||
Version vom 4. Juli 2011, 14:55 Uhr
Es seien 
ein gleichseitiges Dreieck und 
eine positive reelle Zahl, die kleiner als die Seitenlänge von ist. Ferner seien die Punkte 
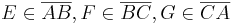mit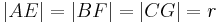 
gegeben. Man beweise: 
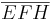ist ein gleichseitiges Dreieck.
Auch hier wäre die Definiont des gleichseitigen Dreiecks gefragt.
