Lösung von Aufg. 12.1 SS11: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 10: Zeile 10:
  
 
Lösungsvorschlag 2:
 
Lösungsvorschlag 2:
−
In einem gleichschenkligen Dreieck sind jeweils zwei Seiten kongruent zueinander, diese zwei Seiten nennt man Schenkel. Die Basis ist die dritte Seite, sie ist nicht kongruent zu den beiden Schenkeln, die an der Basis anliegenden Winkel nennt man Basiswinkel im gleichschenkligen Dreieck.
+
In einem gleichschenkligen Dreieck sind jeweils zwei Seiten kongruent zueinander, diese zwei Seiten nennt man Schenkel. Die Basis ist die dritte Seite, sie ist nicht kongruent zu den beiden Schenkeln, die an der Basis anliegenden Winkel nennt man Basiswinkel im gleichschenkligen Dreieck. --[[Benutzer:Phil86|-phil-]] 17:29, 3. Jul. 2011 (CEST)

Version vom 3. Juli 2011, 16:29 Uhr

Definieren Sie den Begriff des gleichschenkligen Dreiecks. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.

Hinweis: Die Schenkel eine Winkels sind Strahlen. Die Schenkel eines gleichschenkligen Dreiecks sind Strecken.

Definition:
Es seien \ A, B, C drei paarweise verschiedene Punkte, \overline{ABC} heißt genau dann gleichschenkliges Dreieck wenn folgendes gilt:
(i) 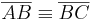\overline{AB} \equiv \overline{BC}
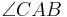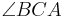Die Seite \overline{AC} heißt Basis, die Winkel \angle CAB und \angle BCA heißen Basiswinkel, die Strecken 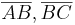\overline{AB},\overline{BC} heißen Schenkel des Dreiecks.--Peterpummel 20:55, 2. Jul. 2011 (CEST)

Lösungsvorschlag 2: In einem gleichschenkligen Dreieck sind jeweils zwei Seiten kongruent zueinander, diese zwei Seiten nennt man Schenkel. Die Basis ist die dritte Seite, sie ist nicht kongruent zu den beiden Schenkeln, die an der Basis anliegenden Winkel nennt man Basiswinkel im gleichschenkligen Dreieck. ---phil- 17:29, 3. Jul. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._12.1_SS11&oldid=7956“