Haus der Vierecke (15.07.2011): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Definition: (Raute)) |
|||
| Zeile 46: | Zeile 46: | ||
* Ein Viereck mit vier gleich langen Seiten und einem rechten Innenwinkel heißt Quadrat.<br /> | * Ein Viereck mit vier gleich langen Seiten und einem rechten Innenwinkel heißt Quadrat.<br /> | ||
* Ein Quadrat ist eine Raute mit einem rechten Innenwinkel.--[[Benutzer:Kinder Riegel|Kinder Riegel]] 00:05, 16. Jul. 2011 (CEST) | * Ein Quadrat ist eine Raute mit einem rechten Innenwinkel.--[[Benutzer:Kinder Riegel|Kinder Riegel]] 00:05, 16. Jul. 2011 (CEST) | ||
| + | |||
| + | |||
| + | |||
| + | <ggb_applet width="1600" height="746" version="3.2" ggbBase64="UEsDBBQACAAIACQN8z4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V1bc9s40n3e/RUqP+ybOOhuXOtLZiuXmUwujpM4l6q8TMkyLSuRJUeSncuv/xokQZsybYs25TFYO7sV2RRJk+c0DrqBRuPBf38cTXqn6Xwxnk0fbkEitnrpdDjbH09HD7dOlgd9u/Xf3//9YJTORunefNA7mM2PBsuHW5Tglj9+Mv793/96sDicfe8NJtkpH8fp94dbB4PJIt3qLY7n6WB/cZimy8rxwcmP8WQ8mP/c2fuSDpeLsy/ymzyfHp/wX1nOT/jY8Gj/1XgRfv0t+4PHk/Hy6fh0vJ/Oe5PZ8OGWVvzo/NPHdL4cDweTh1tS5Efw4RaufMmHyH97OJuPf82mS3/62c0ng710wgDsLn9O0l7v1H9L+VcHfHKvtxj/Shks9Mce/JZh8CA9GU7G++PB1L9n9oh8Uq/3fby/PORzdfbn0vHokN/DSJnfbjibzfd3fy6W6VHvx+d0PuNHtS4RUpNFIxCtVVu9n+EbSMhphaisIW3BML78MvwoKBKrhTJCWGE0gpV81eXfZX87Pd1Nl0t+zUVv8CM9Y2A0H+8H5P3PzxePZ5P98uvj2Xi6fDI4Xp7MMxuh4lAG1sMtfsu5f8lH09EkLY4hU3iYDr/uzX7s5shRfuv3P4+zS7Ln2Rs9mU1m897c08VvPSo+9/LP7Bz/oOVZIjtHZGcU9/A3Lb8Hh9kZ2ede/pnzO57mj1a8OISXBhH+zHjR8wf45t60y5fPLOPh1lbvZDpevgq/sEl9LV4V8gtenxztcZs6b1TlPaGtez74bcXmHnxN59N0khvWlKk9mZ0scvPN/1b2IPvpcHzEv+ZfFJAMPF0f+AHyo/vpaJ6GB89bZA5Y9q04b7wrhx/8Fh7CP8OCn3W4ZGnh91n6d/Etf8mtzv+0P1j6I77tTNKjlBvWMrOHzJxKXB5tlQIzy7Qi2Gbx/RnC/HWtbWRWNJgcHw74SCJCG//JynH+dbL7bc/2qy85mDJY2RtwIz32N/B0HKfpfqGWy8KGe8d8y6xFnMM6g2jR++FNKxFaalCK/08kuQX85KOQGE1akRHc3q0Fvvmv/MbZ9XnL8kJyJkJMew7XNcA97ghwMmHtMijJgdLSSZsjh6xqrGaImoRC6RWvLeSedAQ5lxinrCNwUiMakwMnEv5R+X5EGWWM72DaAu5pN4BziUXpuO81DB0Q5sDZRKBUEoU1hv/FhgY3nB0dDab7vengiJ/hzWzyczSbZniNva/TGwivdb0B+JbbG6A3w96APKg5YifLcBqr/YS7U8jPHuRn7+VnD/lDsoDnf774ozW05X8+EFPesdo9Lg+5F5qmi0XWhy/P99aXk3wO0vMsg6KMZwVFh31GMzSh+XJbXKQj/1v5IIN/5m0aGu2Z2fUhAcENwColDTt4BlVmeCyAQoNgc9SCQIHLDK8vIXEA0mipfOMWIFe9myteOP02zc9Z5D7G+Igd6uF4WdraxLeP59Mlexxp1oNfdCS+pumx9+B2pu/ng+nCRwb5OecclDWp2ouMKkyUtdyZGzLI4upcRpRK2DUHba3gLslYpJwoEDLhk4AMOYkglI2XqGF0RKFiMqQkK5guDRlRfZc4I5yWhCAJpMy1XJmE2xghMYtGc9eo4yVqPzKi+pRw8wAAjUKx9jERGVXsrXDMy66eRPKNhzvejCuSiQUCEmCA2KGmiLiqOk1/XOM0XULCvfOauPtyzBMhCm5XmiTIjEHitmaNs6jRcojjqD1/88+OQCcTAWzBht11zR2/cpsG7llHgNP+3J/5A7QGzl8dAeeyBtnnJ+LAmZWTDCCAYGezoW2tE8z8kYcnf+bhybM8PPnrsmAG87PT/OyD/OxRHswc3iiYwU4FM2lk/bkoWqYuWmYfiZ0rNNYpwx9R9derXBxExkVNR+IHglbVoXM8jSLjqV6XvWKbeq5YbdCwUyyRP9hF1hEPARxGRlafnbbKf1DxRDxlUiu0lunMIpp4qKm6Q8874g75ge/zYwEqn0jwPCJ73Uo5IGkIWpxIeNEV6GwFOgsbR+5lV5DTVaMrbM6uINfitN+rjiBn61vrLZFbJ3B5nociL/JQ5GUeiry6LHCh/OxxfvaX/OyveeAyuVHgQp0KXMaR9eshcLHV7l0Vw46YIJC1bHrsnlkDEbvHXyJjhsOYyn+mcI6xyhQWqQB9y6qglfYBjzTKXMz+iYeqr5FRFRpRf6UVhSkxLSvNKCbneJWaSWTU9C9pRlgELtJVWk1MIWXVEdruiCNEWDQm2eYg9+uOoIN2E1MAOx1Bp7Sdvm0TnjddgefG80frxBHbeWTwOo8MdvLI4M1lcYTMzz7Kz57mZ8/yOOL4RnGE7FQccRRZPytDywuy3QfA8nYR9KarBEwjI8CudJt9RBkz/rPI8O+vEoDWxoz/cWz4X1AgkFE1gKrP8bYrPgcmPuWQlFMaz0aEuW/ggxbAWSWFQt2et/auI8ixq1+LnN4YcrsdQe4Sm0OxglyLEzjvuwKd3oTRrRM+vM0Dgnd5QLCbBwTvLwsfVH72t/zseX72Ig8fljcKH1SnwodvkfXeNeGDsQkJ4RwYraWVEPF49jw+Nir/ka6GFtIloIR0ylpCiUjxUrOIjJoLeTgr3CCISrOhiAa0V7lZRshNVcUsVBpKPFRUvZsPHfFufCq4BhIKUIJEPxfniiRxgMRpJUlIbZA9HGrRr/7YEfhM4shqJ61RVhnHPfLGofvUcejMCnTtIfe5I8hd1WZvh946UcmHPM74mMcZn/I44/NlUYnOzz7Jzz7Nz/6eRyW/bhSV6E5FJSeRdeghr8Os5BBkduZUYpCkJENGSzARJ3WcRsaLWuFDVXPRpUk0IWjHAgbSxOR3rTLzPTJmykyo2ibTB0mVRqNVvNT8ioya/jWthuNGbSwJI6VVyF2qiCisXymi9Td0xPuBkLLRh1ZTWh53BiEUm0HoSQcRQmwToaedQeislTVHaK1CV38XxaseZz9gbl15uau/4bJowhQFr8I1e+GaYfaDL3uVX9w4qjCdiioGf/9Dhbxu7SWFYUITdabUXnT4h3Ha0vexImYChtERUPZI5ZRS3MlS+9Ex0F9tAzriZKk/OuOJ9PVqy2inclRnALqgHO0UiOoMPptZAfFXZ/Ap03SbA7RWFajg6f8ZvPZnwWv/63JP3xbVoMI1B+GaUfD0D2/o6dtOefppdN3sal2ouHPyD6LDP3g5IayP2sscRQf/2dhcR0Ktw+go6K82gX422hUNAyvVmTrjiNiVnqGdCkydgUclRiCB1SidMGCwqBEryAnlnN8tSN8q3+MjYzObr9bCCe7bixpn7eQ6H+w0v2WZ7bBRrTjPWDtCgQk6oy2QUcKh36AlFBxxWjgphOHvyWSgNxPxc1vnFCIyHMyX6WI8mBZvv+Tf33j+eumP45yHBmb/sjNm3+eThWWLJy20AW0VhiK2xinHNq+ElIYIW9zH5FV34BOZrRohfPFIQl1sn9OnRFohQRsptbHWqFttZ1KrHS+Ddryq0Y7ThtpxGpd28KXSODKEVmorMWSls3bwr6zgfisIAiXpLtTjZTP12O6M+ctEO6VJGu4ejSBZFsBWwhJ3p8Zpv5GeaLH+3uvOgGcTCxbZWI0ixR9lvUy/FZcmAsk2jk033lpDOLaDcLyuEY7vDYXje1zCIRO/pRkIlJahBSWDXDsSlpWcbRgYdnkXsrHdTDZ2OmP5DDfLBYLfVs67fxp1GCJVGowhpdHbP7kWa+p0Bz2RaFRSWO79HEp2PMplEYqIfQ0OVrhnZL+tdeXYCcrxpkY5fjVUjl9xKQcmUrJPx8EKWOsk419GKwaBjVUz4ii0uhPt2GmmHW87Y/2ACSOtOTa0vpS7Fnbj0vGuM+DZxLCbJoxmp5l7u3K1PSQG2Y8zKFmTDTTds3IN5XgblONdjXKMGyrHOC7l4O5OOYWOnWEFHJSQoOB1sJ9ntU+DdqCM1HehHG+bKcduZ4zfJV4wWKcFcURiNZZZvHzM+t0ftEXdtNe8skhHZ7ADlQglhDPa+AFSCKNE6Bd/awkccBvBnWLTpZhrKMduUI73NcrxpaFyfIlLOVTCDjIHh8JX/zfoCotNLIfdSnFgzSZLTt7JEOluM9340BnbR5dI9qmJeVDsbutyNahlP9xq8L64duwEtqgcH7uDnkic87vqMEhEhJZK5VCSA3GljfO+c/vByocgHB9rhONrQ+H4GpdwsDvMsbWfyCJ2LYQs138njrtAR3zY+JE5DXchHR+aScenzhg/Md4GHHt27F4LUGG4ybKuO/IDf6zr4FqsX/C589hBVuKEzdo71KhB3mqLklrl+BSU43ONckwaKsckLuU4W7tVrYZl70QpPjVTiid/Y0es3a8l9HvMO/YvjOJI0eQs6EQKqRwZy34G/6/FmZSnnQGPPTThlCGZdW467OoHlFiLFoxAJD/o337+hjfATCk8mKtKMW2oFNO4lIKFWDD9lpXZsDOhXbmZojTWIy6B4xZl8S6E40mO//oLODpj+yHdrsx4bGkBR2cACisUWl2g8Kw7+Kzma7a0gKMz+Nib2s966zcwrN/AsH4Dw/qNi11KscrChfUbGNZvYFi/gWH9Bl7d91yyfsN1bP3GP7RL+S1mGUv3WxTbKkS9hOAgOgb0ihz2QUbNwCg6Bso1qeWSS4pqBcHFNRzRMVDKUFlYNqo2sFqdqSu+CLiEQCtwTjhHVul8lMAlCs4WKQhl2qzb1BXsEBJCZ60xQmlALHLO/IbHUkkU/AX/23QSZ40xgkfBxXtc49AdNRwjOIprjIB1BIi0MY5tlbQqZzCl1WynYP2QliC6k8yHR83GCJ53x/RN4pNejQNhEI2jvBKfSsCXc1dCAWhLpsWUqRfdwY4ll1gfQClnKatvn3uHgGy8QvsJYE1A7adMPQ+68aJGN44b6sZxbLoBwqFkZfbjttJZ9U8mWz6vEY4fx3O+ubevkOyT/liyiWUX/OfbyWz5f29PBvvzwTL/JbtBlaIlX7FVvfxq9IPjsxHwz710UaLOgdOKWKkVGCXNOhk/10OEFYjepcPDZTr8uj5GLehKeyBhIh2rp2FtVUhChAUwoBI06EueSi+66FQzkKgC0mAyGSU9doKP01/rA0X3CSi+3nGbBXAShN/UqUjbhcRadmOlkGQsiyw2w0lWcHozmDNU6WQ2mg+OjtZHSt4npHwWP4AyToPyy9r82ql8IhDlufxm2RApVUFqNGluT+o+ocRxqQ+E/CIzyXGPLmoLe5S4X5Z+0SUblCXTDCVdFafByTJdHyB9nwAi8AshSfku0ksQhQQgnUgkycJEbGVItqEdmQpCi59HSe/pfDA8bICTuVc4iYSlx1nBTgV7ciB0WMJoHfBRIQw7fWCaKpOt4jQ8HKcH/HxNsbL3CSvExKAQWZ0Edg0k6GKzAtCgjeA+kNhXU5e3uStX1F/XsV/v/NyLeKHf0nTRk/F8OEkvLPkuQgIKNz0XEny7LiQYzqbjYYnnt41GBH40clRQcjsjXG+8cTxKp3nIs2BbFQVnP8XDot5kOPID8h1e+DsoDv2CcySxDczHP3qPwvmPwlmP0PfNLvuRirs+kgXNj1RBfO3gJ1vRcHzA0F9JeNbOVvj+VpN/9ur6mb1qrYUbeszgKz6Mis9707pAJOiQtVoCGsWudRgBdRykswBxZ8cf2HAE9GZMbDdjYrtbTKiElPMbNyg/Hs0+aUEEB+1aGq2YBL/11F0Q8boZEa+7RoQ1VnPAwHGUFKRMMbhXPWrvgoidZkTsdIsIl/hBbm4K5JO7sRxl5WBNgN/qxLFg3a6IVH0SyavgFmyHhJDXISFk5/IkEhD5RZNw0VG4aBqySGY3zCLhW2/OtcjIPnP6/IK9TeeRTDY6g3vVC914BFX4OUGLRnN0bLx7jsWUuiNENk9lWLd1sfSg77dJkobDHA3Oz4UFHCOY613l6ig+rihRUjkWa2f9aj/nyjI6YJlCVg+fSxv2j0fi2FRptFYJtPwZL1fT+Ljy4wVaM+oGpV+DoqAsIaOtNeAXc8tsmlmGArzoR4j9hpGSCdPxsjWLjy1fTcmRZEdUk3Na6rJCFdPH4YLf3RPAr+7MdZA4wJPsMhlubr4fj3ZHsjedmYD1W7+TFRqN1BRKjPlkdzJOeMGUoLRtcV3M285Ax9bvC7ER+rJAWpNRd5Ty8iY4pG9r3M95w6nreVxT137ZEfcPQFYDBwLOgikzeiu5MOZOahO+aZb08q47xm8SZfy2rKSFlQotFA6wNOzoOtZ94cuutLhof7c72KlEK792DhE5iuAesaxqSuiH2IANXEi1gayXd0E6dmukY9FQOhZxSUfd6vxib1vhtHLgDFrHEqLuQjnerZv14ipzXbvp4TSdno7TeaO8DnefZrr6LvEaceZe6KJ0ulPWeP+QSbBZBbjmM13vuzLTRZuc6XofZKDcqfCcDCybzXQt/zfT1XimSwl5YaqrT7eY7Lq6VlBXOs6yTUCrqyk/dgcg5QfJOZZDLQz5mrtFDoFDjlCM5CNCgW04SH51NZnOYMfGBcheK/+rERXKwqM1+lxh0qYl2K6uJtMV7KRIJPfjHIxp6dMQTRtmt87czIfQkX0M0yyfwjTL5yvmZooCNCfhotNw0fcwN/PrpnMzm+wMwyBe6A2r3G9oduYkvnFJ7lwN+E01NDv18twQAcdXBpUhh1qH4LQPyKrpRymtURaFECaeYclVsk7jI2u1TKsxxRKQSkFosgVZvnCVr91PPnXQShkxWd/jI+tCUd16tmQxciFsokEL5Lg6y//EeMn6FSFZl+vg+c46K7np2bIyAUfIDApSUt/rllV1DnYLsq5wDlZdgcF1HfyqAQw2agCtj3Z1uQ9ch/yPgfxPNeTvNSV/Ly7yu9ynrkP+56vIHzYlf9gJ8vv1fXQ/rk66Efsfatjfb8r+flzsd7nTv7oMSQtLMu/FYApsZpTzcWcAIp0QSTSgQCMaC6pIjmcBE45Vz68sqy7hbKnUCIVSI3RBV8bX6cqFXVaikhU2yjrM+76UgHICs3XHrsiD33ilkUaG/6RLhi/a32X6aXfwkQlxH+f3GGSTRGULr9dvnumsRsPOECl7q1UzlxQqplCo+KIyfGmoDF/iUoY+JNqvdubWz+JrJGK5/xI6rQSQ8bMpWsKdZGQ9qRGH+moiopJY8X4wHfHpN8itKJZj3JPkCjKJUJQVMWAfMGxNoRNtkemwTmjUqOgmuRV/dEYoIAhpv10f68/OIIRiMwg9uylCLY6QbgCjVjvkvzpjRefaWWOE1qvvTKG+M4X6zhTqO1/sicMcLYYCzxQKPFMo8EyhwDNd3WdfNv37T00SbKzEM8U26xEaZaitGnd94YP4CAgV78OOCX3bzOW7ZwyM4mOg7JdCG+hrGTMFh/FR0F9tBXExsFqr9TqHJJKk6nJotQ+yTY/tRR1A+RNE57K5RGrB8SPH8yTJYtjFerXo4q3WtdVmpT8P3tyLGt/t63WjKNWs9K8bHUTpZFa6Al8FUTvmVmip/cRRNUEdygR1KMXsZtWYrqb/WQ39x83oP/4f/c3px4trEm5D+dUF6ToT4vr1voiAfhtYBxgmRsD4te7a+n0HUYK91Vq+ugpBg9rqZdeGrdXqZTdk4V5WCDrXud9yzVTtGP/LIE+vauTpW8Mx/m+RjfGLVSOXqizl6fw+uw6dTx0D6e6kZvjLZlOA2/dbbtZfOawT8AvffSEbX7rdulB2SGmlSGi/Jhug9WpkxzWJNK+bac3r+6816yuNStjg/c6xBoRAKUJhcl+bQJBAi1IJt4mZxu2gQq9rVGjeUIXma6kQ3hsZ8pvMGAtW+oIlmjKtKfReg7ZKWXZeDRrRaMMTvKkIbTcToZ2OiNAliwx14hAcCxP5eUZSDR2eq8vtdAM55M5SamIrNcZqWQDnZ9isYVUndhR91SvT/k7KO0E23tTIxqKhbCwikw0/2KNRWKvAovUT4cFHd4lxFkBzvym568S70Y2dtVMUoKb2Q7/MVOh/bJyqcN0eKHe7GYNL2J0kx76kZudRwhqR03nQ2F6nC378bPjT/z5KZ6N0bz74/f8BUEsHCJF8LKKXFwAAGQgBAFBLAQIUABQACAAIACQN8z6RfCyilxcAABkIAQAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA0RcAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
Version vom 19. Juli 2011, 01:00 Uhr
Inhaltsverzeichnis |
Definition: (Viereck)
- Ein n-Eck mit genau 4 Ecken ist ein Viereck.
- Wenn für ein n-Eck n=4 gilt, dann ist dieses n-Eck ein Viereck.
- Es seien A,B,C,D vier Punkte die alle in einer Ebene liegen und von denen je drei nicht kollinear sind. Unter dem Viereck ABCD versteht man die folgende Punktmenge
 vereinigt mit
vereinigt mit  vereinigt mit
vereinigt mit  vereinigt mit
vereinigt mit 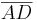 .
.
Definition: (allgemeines Trapez)
- Ein Viereck mit zwei zueinander parallelen Seiten ist ein Trapez.
- Ein Viereck heißt Trapez, wenn es ein Paar paralleler Seiten besitzt.
Definition: (gleichschenkliges Trapez)
- Ein Trapez mit einem Umkreis ist ein gleichschenkliges Trapez.
- Ein gleichschenkliges Trapez ist ein Viereck mit zwei parallelen Seiten und Kongruenten Diagonalen.
- Ein gleichschenkliges Trapez ist ein Trapez mit kongruenten Diagonalen.
- Ein gleichschenkliges Trapez ist ein Trapez, dass eine Symmetrieachse besitzt, die verschieden ist von den Diagonalen des Trapezes.
Definition: (Parallelogramm)
- Ein Viereck mit zwei Paar paralleler Gegenseiten ist ein Parallelogramm.
- Ein Parallelogramm ist ein Trapez mit einem weiteren Paar paralleler Gegenseiten.
- Ein Trapez, bei dem sich die Diagonalen jeweils halbieren, ist ein Parallelogramm.
Definition: (Rechteck)
- Ein Viereck mit vier rechten Innenwinkel heißt Rechteck.
- Ein Rechteck ist ein Parallelogramm mit einem rechten Winkel.
Definition: (Raute)
- Ein Viereck mit vier gleich langen Seiten heißt Raute.
- Ein Drache mit vier gleich langen Seiten heißt Raute.
(Geht das auch mit weniger genannten Eigenschaften?--Tutorin Anne 13:08, 17. Jul. 2011 (CEST))
- Eine Raute ist ein Parallelogramm mit vier gleich langen Seiten.
- Eine Raute ist ein Viereck bei dem sich die Diagonalen gegenseitig halbieren.
(Hier müsste noch als Kriterium hinzukommen, dass die Diagonalen senkrecht aufeinanderstehen oder Definition über den Drachen, s.u.)
(ja eben, so ist die Definition nämlich nicht richtig!--Tutorin Anne 13:08, 17. Jul. 2011 (CEST))
- Ein Drache, dessen Diagonalen sich (gegenseitig) halbieren, heißt Raute.
- Wenn bei einem Drachen beide Diagonalen Symmetrieachsen sind, ist es eine Raute.
Definition: (Drache)
- Ein Viereck bei dem eine Diagonale Symmetrieachse ist, heißt Drache.
Definition: (Quadrat)
- Ein Quadrat ist ein Rechteck mit vier gleich langen Seiten.
- Ein Viereck mit vier gleich langen Seiten und einem rechten Innenwinkel heißt Quadrat.
- Ein Quadrat ist eine Raute mit einem rechten Innenwinkel.--Kinder Riegel 00:05, 16. Jul. 2011 (CEST)

