Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz (SoSe 11): Unterschied zwischen den Versionen
(→Der Zentri-Peripheriewinkelsatz) |
(→Definition XIX.1 (Peripheriewinkel)) |
||
| Zeile 3: | Zeile 3: | ||
Wenn der Scheitelpunkt C eines Winkels <math> \angle ACB </math> auf einem Kreis k liegt, dann ist der Winkel ein Peripheriewinkel. --[[Benutzer:Teufelchen|Teufelchen]] 16:28, 17. Jul. 2011 (CEST)<br /><br /> | Wenn der Scheitelpunkt C eines Winkels <math> \angle ACB </math> auf einem Kreis k liegt, dann ist der Winkel ein Peripheriewinkel. --[[Benutzer:Teufelchen|Teufelchen]] 16:28, 17. Jul. 2011 (CEST)<br /><br /> | ||
| + | |||
| + | Wenn der Scheitelpunkt C eines Winkels <math> \angle ACB </math> auf einem Kreis k liegt und seine beiden Schenkel den Kreis schneiden, dann ist der Winkel ein Peripheriwinkel. | ||
==Definition XIX.2 (Zentriwinkel)== | ==Definition XIX.2 (Zentriwinkel)== | ||
Version vom 17. Juli 2011, 20:19 Uhr
Inhaltsverzeichnis |
Definition XIX.1 (Peripheriewinkel)
Der Winkel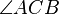 
im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:
Wenn der Scheitelpunkt C eines Winkels 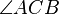auf einem Kreis k liegt, dann ist der Winkel ein Peripheriewinkel. --Teufelchen 16:28, 17. Jul. 2011 (CEST)
Wenn der Scheitelpunkt C eines Winkels 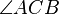auf einem Kreis k liegt und seine beiden Schenkel den Kreis schneiden, dann ist der Winkel ein Peripheriwinkel.
Definition XIX.2 (Zentriwinkel)
Der Winkel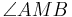 
im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:
Wenn der Scheitelpunkt M eines Winkels 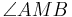der Mittelpunkt eines Kreises k ist, dann ist der Winkel ein Zentriwinkel. --Teufelchen 16:31, 17. Jul. 2011 (CEST)
Bemerkung m.g.:
- Nach der Definition wäre jeder Winkel ein Zentriwinkel. Der Begriff macht erst Sinn, wenn er als Relationsbegriff aufgefasst wird: Ein bestimmter Winkel ist Zentriwinkel von einem bestimmten Kreis.--*m.g.* 18:19, 17. Jul. 2011 (CEST)
Idee des Beweises eines Spezialfalls
Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?
Der Zentri-Peripheriewinkelsatz
ergänzen Sie: Jeder Peripheriewinkel ist halb so groß wie sein zugehöriger Zentriwinkel.--Zeqiraj 19:40, 17. Jul. 2011 (CEST)
Satz XIX.1:(Der Zentri-Peripheriewinkelsatz)
Der Peripheriewinkelsatz
Satz XIX.2:(Der Peripheriewinkelsatz)
ergänzen Sie: Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--Zeqiraj 19:39, 17. Jul. 2011 (CEST)
