Verschiebungen (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Definition über zwei Geradenspiegelungen= ==Definition: (Verschiebung)== ::Die NAF zweier Geradenspiegelungen <math>S_b \circ S_a </math> mit <math>a || b</math…“) |
*m.g.* (Diskussion | Beiträge) (→Definition: (Verschiebung)) |
||
| Zeile 2: | Zeile 2: | ||
==Definition: (Verschiebung)== | ==Definition: (Verschiebung)== | ||
::Die NAF zweier Geradenspiegelungen <math>S_b \circ S_a </math> mit <math>a || b</math> heißt Verschiebung. | ::Die NAF zweier Geradenspiegelungen <math>S_b \circ S_a </math> mit <math>a || b</math> heißt Verschiebung. | ||
| + | ==Eigenschaften von Verschiebungen== | ||
| + | === Verschiebungsweite === | ||
| + | ====Satz==== | ||
| + | ::Es sei <math>S_b \circ S_a </math> eine Verschiebung <math>V</math>. Für jedes Paar (Originalpunkt <math>P</math>, Bildpunkt<math> P'</math> bei <math>V</math>) gilt: <math>|PP'| = 2|ab|</math>. | ||
Version vom 7. Dezember 2011, 16:32 Uhr
Inhaltsverzeichnis |
Definition über zwei Geradenspiegelungen
Definition: (Verschiebung)
- Die NAF zweier Geradenspiegelungen
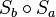 mit
mit  heißt Verschiebung.
heißt Verschiebung.
- Die NAF zweier Geradenspiegelungen
Eigenschaften von Verschiebungen
Verschiebungsweite
Satz
- Es sei
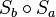 eine Verschiebung
eine Verschiebung 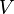 . Für jedes Paar (Originalpunkt
. Für jedes Paar (Originalpunkt  , Bildpunkt
, Bildpunkt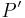 bei
bei 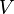 ) gilt:
) gilt: 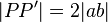 .
.
- Es sei

