Verschiebungen (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Beweis (Parallelität bei Geradenspiegelungen)) |
*m.g.* (Diskussion | Beiträge) (→Fall 1 g \cap a = \{S_1\}) |
||
| Zeile 36: | Zeile 36: | ||
# Der Winkel zwischen <math>g'</math> und <math>b</math> sei mit <math>\beta^*</math> bezeichnet. | # Der Winkel zwischen <math>g'</math> und <math>b</math> sei mit <math>\beta^*</math> bezeichnet. | ||
<ggb_applet width="641" height="451" version="4.0" ggbBase64="UEsDBBQACAAIAEuQhz8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAEuQhz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VrrbttGFv6dPsVAKPZHEFFzHzIrp7DTOHHgNMW6u1gsFltQ5FhmTZEqSfmS7T7Utn2OfaY9M0PqRlk21cQKEsQZXs7czne+75xhPPzmZpKiK12USZ4d9IiHe0hnUR4n2figN6vO+37vmxdfDcc6H+tREaLzvJiE1UGPG8skhos4iDEh530uZNTnMeX9QAW0H58TNlLc930sewjdlMnzLP8unOhyGkb6LLrQk/A0j8LKTnxRVdPng8H19bXXTOXlxXgwHo+8mzLuIVhmVh706ovnMNxKp2tmzSnGZPD3d6du+H6SlVWYRbqHzBZmyYuvngyvkyzOr9F1ElcXBz0pVA9d6GR8AXuSGPY0MEZTcMhUR1VypUvounRr91xNpj1rFmbm/RN3hdL5dnooTq6SWBcHPewx6iupCG3aHsqLRGdVbUvqOQfNaMOrRF+7Yc2V83IPVXmejkIzIvrlF0QxxeiZaYhrKDRSulfYPcPMNdQ13DXC2XDXnTtT7my4s+Gsh66SMhml+qB3HqYleDDJzgtAb35fVreptuupHyx2T57BnsrkAxgz41LncniO8TPzA35+xhtfL22SLM1aFbOOkzZTSk4ePiX9QxtlzZyUyPacVNyxTbllUrfvh+yTiCXXwlT2r/1pzci2bXN9Rnf/xyaU/FG2OBw0VBnW7EDlhbGto6fSk9LwhQVIBCbsCRLADakgygUiATSKImADIgJxAbfER9K0CjEFLzhiyEfGjjBkySF8+IcrO5hEAgYzTxVwEhGYiCPBELGc4giYhCwvgaOUgYUQSEAnMz2hZggmEZdwx3zEYY2GkoqAIYOOcA/TU8QIYqYzUYhKJM14hBuqS98sHYakSGIkiRkQWA2MdmwGex8xsxtZuyvJprNqxUXRJG4uq3w6xwKsQY8Wquf0aUUUnwzTcKRTyBNnBkmErsLUMMJOdJ5nFWpA9N2zcRFOL5KoPNNVBb1K9FN4FZ6Glb45BuuymdvaRnlWfl/k1cs8nU2yEqEoT/F8zXlKlq7pfNVww5Ze8OUXYumFXLpWG+fN4Q2alRrmz4uyMQ/j+MRYLKQBPPk+S2+PCh1eTvNkdRvDgU05Qz2L0iROwuxvEKxmFuMXNM9ARq6aDMQpaxaSF/HZbQkRjG7+oYsc/KioxyWRzOfCJ1gpUJ9b94oGgaekHygRYME482FpUWi4R31PEBL4TPoSB1RAlzve4HpmfTUHKLzRi72OC0PspZuT8ihPF4/s9l+G02pW2NoBVleYTR1m41TbELFqC4k5uhzlN2cuNpgb64fbKdxht4LR2LodgTRQASse1+3ItdbGLG1uha0Ntha4CbYknr8nAbUWth251lpB9Lql1VslzTYJbqZJSitouFfTphErE/smz8+ypDptbqokuqy3SlyH72aTkZ5H0OqY5GONORyshdjwUheZTuuIBjBn+ax0BF0K9lhHyQRu3YvaJaGB66+wAPc01uNCNwtPbV3mHGbf4uVgbT22Qx0X+eQku/oBYmFtAcNBs8phGRXJ1MQcGkEWuNSLqIqTMoQkEi/3MxSErUcmWYB7KuMaIOesusgLW3qBpkBrLSeTMItRZvPO9yZCewsdDEFRbg4BDbfcfFY1Tw/d+uruhsKpnkDFhiobpzbU53gd2iENMCgf/QT6uA7oAnp4vwhK6kLbtnVoozCdXoSmZqxdmIa3ulhxqh3zXR6vuxqQtP4AxZiaAUysTLV2YeaWDRdTGNCyc0XzAL0S3Zjqn3LJmQgE5VwoTqE2vnWrQR/c4cBVx2b/hsArmu+erkUBhKZzXQuN9wXgNc6zMD0FFq7BcgiuIHehE25Hx5B67vuwDU5d32zDZlVQHorK+/PzUlfGkX1pHUeDjZixdb/37bFrxdMtINb0qoJMegnHhdKKalXLp714k8SxtlWU0/OfM9eldCKSTKZpEiVVvQgQbBM2dmFfh19vx+zhDDrqwqCjz5BBu/BHeT4W2CfSx1wEAab7os/RNvqMOtBntB/6OMcxsSN92jg8CntGLfZsC/qXuwX9sm/3HvB95nHBGKdUBkoqSWrgPE4DzH3BhPApFJgfJf63OfPbL8CZzBOBZFCIS3Ab5ZRYX4KLhcBcUV9wQqng/BOIyQYJeekk5NuWfIw7yMd4L/JBuMu+/GHyIb1AQaIlDM5PmAd1DCsPrqVUDP6YL2nUur0Pq1AYzlkUK5/7cN5i7HHEZXxPaj7JKjgTgIvXcAwdjuMWjmddMvTZTkCar0Bj14xc0z0V1GDyB+YC31O+DITvEwWYscD17vueBALBeddnBOoq8wXuwyaMu1JqHaWzH8kOJVTYAudVF3BefSHl0x3HD+IpYgQwAEgBQEI/gQBuQqVNmeMuqBx/IahAdUU4uJ9iyD2CMoGDGhZgEguAP0IGjFD/U+BiPx6t4fLKKdoZNLTGZAWl//13O0z2s8QcBbA2/WExs2ZJngowCyDQiAK1wLLOI13VTxALpGlaOIoHy5/jQJ9s1b9dkk9YRAt0RBMwaZpf/0Wfp/rGut69XexvVe3+afdzj+C9S4oiL1rcshi2hW/8I+lSX4D1PioM4TtUqL9biVGXduv5h7kagyjzX4ZYKdBAwoQKdge5U4Xxr6e7QHl8F5THfwqnefnnTppZd9m/ci6X5ZKZOi+AH858Julm+Xsk9WtctKyBr9oa+GsnDfz1c9bAWgHp56uA9xLnruLc6JcFctRC8HUX3rzeV3leV+fkgR86hfAwZZQGTEhpNM51ZwrIpAyRJMPwVGyszllnZrWrc7pTsrobpahDsor2cxh2ciUfiFCnw3BA4FgFIkgExiQg/qMlqn8/ffqfg7FTwh3OW3WRsYLkmy58e/MZZKiPUdsLDxgnFBNw7oKTMSbN5zsOuAqiAHCfK6we6cTV5tdJF1ROvhBUNv83AvWEoJRyyiExM2ZS8uOgErVQedsFlbdfCCqB51MqARfBhcRMBjVXqCIBFYEPlSGGOvBTcGVTHfjGpaTXrgI8aVeAv3WqAH+7twKU+zwFM+ds+TmWgCNd3XcG3gTgyQqAb9sA/t4JwN/vBXB/+AmH3tYSZJ/obajfB8u/ZGJ/lav+reQX/wdQSwcI5veBqg4JAAAyLQAAUEsBAhQAFAAIAAgAS5CHP9Y3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABLkIc/5veBqg4JAAAyLQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUJAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="641" height="451" version="4.0" ggbBase64="UEsDBBQACAAIAEuQhz8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAEuQhz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VrrbttGFv6dPsVAKPZHEFFzHzIrp7DTOHHgNMW6u1gsFltQ5FhmTZEqSfmS7T7Utn2OfaY9M0PqRlk21cQKEsQZXs7czne+75xhPPzmZpKiK12USZ4d9IiHe0hnUR4n2figN6vO+37vmxdfDcc6H+tREaLzvJiE1UGPG8skhos4iDEh530uZNTnMeX9QAW0H58TNlLc930sewjdlMnzLP8unOhyGkb6LLrQk/A0j8LKTnxRVdPng8H19bXXTOXlxXgwHo+8mzLuIVhmVh706ovnMNxKp2tmzSnGZPD3d6du+H6SlVWYRbqHzBZmyYuvngyvkyzOr9F1ElcXBz0pVA9d6GR8AXuSGPY0MEZTcMhUR1VypUvounRr91xNpj1rFmbm/RN3hdL5dnooTq6SWBcHPewx6iupCG3aHsqLRGdVbUvqOQfNaMOrRF+7Yc2V83IPVXmejkIzIvrlF0QxxeiZaYhrKDRSulfYPcPMNdQ13DXC2XDXnTtT7my4s+Gsh66SMhml+qB3HqYleDDJzgtAb35fVreptuupHyx2T57BnsrkAxgz41LncniO8TPzA35+xhtfL22SLM1aFbOOkzZTSk4ePiX9QxtlzZyUyPacVNyxTbllUrfvh+yTiCXXwlT2r/1pzci2bXN9Rnf/xyaU/FG2OBw0VBnW7EDlhbGto6fSk9LwhQVIBCbsCRLADakgygUiATSKImADIgJxAbfER9K0CjEFLzhiyEfGjjBkySF8+IcrO5hEAgYzTxVwEhGYiCPBELGc4giYhCwvgaOUgYUQSEAnMz2hZggmEZdwx3zEYY2GkoqAIYOOcA/TU8QIYqYzUYhKJM14hBuqS98sHYakSGIkiRkQWA2MdmwGex8xsxtZuyvJprNqxUXRJG4uq3w6xwKsQY8Wquf0aUUUnwzTcKRTyBNnBkmErsLUMMJOdJ5nFWpA9N2zcRFOL5KoPNNVBb1K9FN4FZ6Glb45BuuymdvaRnlWfl/k1cs8nU2yEqEoT/F8zXlKlq7pfNVww5Ze8OUXYumFXLpWG+fN4Q2alRrmz4uyMQ/j+MRYLKQBPPk+S2+PCh1eTvNkdRvDgU05Qz2L0iROwuxvEKxmFuMXNM9ARq6aDMQpaxaSF/HZbQkRjG7+oYsc/KioxyWRzOfCJ1gpUJ9b94oGgaekHygRYME482FpUWi4R31PEBL4TPoSB1RAlzve4HpmfTUHKLzRi72OC0PspZuT8ihPF4/s9l+G02pW2NoBVleYTR1m41TbELFqC4k5uhzlN2cuNpgb64fbKdxht4LR2LodgTRQASse1+3ItdbGLG1uha0Ntha4CbYknr8nAbUWth251lpB9Lql1VslzTYJbqZJSitouFfTphErE/smz8+ypDptbqokuqy3SlyH72aTkZ5H0OqY5GONORyshdjwUheZTuuIBjBn+ax0BF0K9lhHyQRu3YvaJaGB66+wAPc01uNCNwtPbV3mHGbf4uVgbT22Qx0X+eQku/oBYmFtAcNBs8phGRXJ1MQcGkEWuNSLqIqTMoQkEi/3MxSErUcmWYB7KuMaIOesusgLW3qBpkBrLSeTMItRZvPO9yZCewsdDEFRbg4BDbfcfFY1Tw/d+uruhsKpnkDFhiobpzbU53gd2iENMCgf/QT6uA7oAnp4vwhK6kLbtnVoozCdXoSmZqxdmIa3ulhxqh3zXR6vuxqQtP4AxZiaAUysTLV2YeaWDRdTGNCyc0XzAL0S3Zjqn3LJmQgE5VwoTqE2vnWrQR/c4cBVx2b/hsArmu+erkUBhKZzXQuN9wXgNc6zMD0FFq7BcgiuIHehE25Hx5B67vuwDU5d32zDZlVQHorK+/PzUlfGkX1pHUeDjZixdb/37bFrxdMtINb0qoJMegnHhdKKalXLp714k8SxtlWU0/OfM9eldCKSTKZpEiVVvQgQbBM2dmFfh19vx+zhDDrqwqCjz5BBu/BHeT4W2CfSx1wEAab7os/RNvqMOtBntB/6OMcxsSN92jg8CntGLfZsC/qXuwX9sm/3HvB95nHBGKdUBkoqSWrgPE4DzH3BhPApFJgfJf63OfPbL8CZzBOBZFCIS3Ab5ZRYX4KLhcBcUV9wQqng/BOIyQYJeekk5NuWfIw7yMd4L/JBuMu+/GHyIb1AQaIlDM5PmAd1DCsPrqVUDP6YL2nUur0Pq1AYzlkUK5/7cN5i7HHEZXxPaj7JKjgTgIvXcAwdjuMWjmddMvTZTkCar0Bj14xc0z0V1GDyB+YC31O+DITvEwWYscD17vueBALBeddnBOoq8wXuwyaMu1JqHaWzH8kOJVTYAudVF3BefSHl0x3HD+IpYgQwAEgBQEI/gQBuQqVNmeMuqBx/IahAdUU4uJ9iyD2CMoGDGhZgEguAP0IGjFD/U+BiPx6t4fLKKdoZNLTGZAWl//13O0z2s8QcBbA2/WExs2ZJngowCyDQiAK1wLLOI13VTxALpGlaOIoHy5/jQJ9s1b9dkk9YRAt0RBMwaZpf/0Wfp/rGut69XexvVe3+afdzj+C9S4oiL1rcshi2hW/8I+lSX4D1PioM4TtUqL9biVGXduv5h7kagyjzX4ZYKdBAwoQKdge5U4Xxr6e7QHl8F5THfwqnefnnTppZd9m/ci6X5ZKZOi+AH858Julm+Xsk9WtctKyBr9oa+GsnDfz1c9bAWgHp56uA9xLnruLc6JcFctRC8HUX3rzeV3leV+fkgR86hfAwZZQGTEhpNM51ZwrIpAyRJMPwVGyszllnZrWrc7pTsrobpahDsor2cxh2ciUfiFCnw3BA4FgFIkgExiQg/qMlqn8/ffqfg7FTwh3OW3WRsYLkmy58e/MZZKiPUdsLDxgnFBNw7oKTMSbN5zsOuAqiAHCfK6we6cTV5tdJF1ROvhBUNv83AvWEoJRyyiExM2ZS8uOgErVQedsFlbdfCCqB51MqARfBhcRMBjVXqCIBFYEPlSGGOvBTcGVTHfjGpaTXrgI8aVeAv3WqAH+7twKU+zwFM+ds+TmWgCNd3XcG3gTgyQqAb9sA/t4JwN/vBXB/+AmH3tYSZJ/obajfB8u/ZGJ/lav+reQX/wdQSwcI5veBqg4JAAAyLQAAUEsBAhQAFAAIAAgAS5CHP9Y3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABLkIc/5veBqg4JAAAyLQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUJAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | <br /><br /> | ||
| + | Aufgabe: | ||
| + | ::Begründen Sie 6. | ||
=== Verschiebungsweite=== | === Verschiebungsweite=== | ||
Version vom 7. Dezember 2011, 18:05 Uhr
Inhaltsverzeichnis |
Definition: (Verschiebung als NAF zweier Geradenspiegelungen)
- Die NAF zweier Geradenspiegelungen
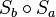 mit
mit  heißt Verschiebung.
heißt Verschiebung.
- Die NAF zweier Geradenspiegelungen
Eigenschaften von Verschiebungen
Die identische Abbildung als Verschiebung
Satz: (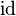 als Verschiebung)
als Verschiebung)
- Es sei
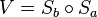 eine Verschiebung.
eine Verschiebung.
- Wenn
 dann
dann 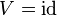 .
.
- Es sei
Beweis (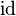 als Verschiebung)
als Verschiebung)
- Folgt unmittelbar daraus, dass jede Geradenspiegelung selbstinvers ist.
Bringen Sie die beiden Spiegelgeraden miteinander zur Deckung.
Parallelität
Satz: (Parallelität bei Geradenspiegelungen)
- Es sei
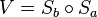 eine Verschiebung. Für jede Gerade
eine Verschiebung. Für jede Gerade  und ihr Bild
und ihr Bild 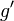 bei
bei 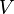 gilt:
gilt: 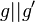 .
.
- Es sei
Beweis (Parallelität bei Geradenspiegelungen)
- Es sei
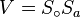 eine Verschiebung (
eine Verschiebung ( . Ferner sei
. Ferner sei  eine beliebige Gerade.
eine beliebige Gerade.
- Es sei
- zu zeigen:
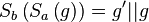
- zu zeigen:
Fall 1 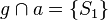
- Die Gerade
 möge also mit der Spiegelachse
möge also mit der Spiegelachse  genau den Punkt
genau den Punkt 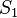 gemeinsam haben. Mit
gemeinsam haben. Mit  sei der Winkel zwischen den Geraden
sei der Winkel zwischen den Geraden  und
und  bezeichnet.
bezeichnet.
- Weil der Punkt
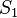 zu
zu  gehört ist er bei
gehört ist er bei 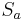 ein Fixpunkt.
ein Fixpunkt.
- Weil
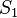 der einzige Punkt ist, den
der einzige Punkt ist, den  mit
mit  gemeinsam hat, ist
gemeinsam hat, ist 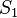 der einzige zu
der einzige zu  gehörige Fixpunkt bei
gehörige Fixpunkt bei 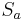
- Mit
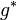 sei das Bild von
sei das Bild von  bei der Spiegelung an
bei der Spiegelung an  bezeichnet.
bezeichnet.
- Der Winkel zwischen
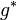 und
und  sei mit
sei mit 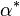 bezeichnet.
bezeichnet.
- Das Zwischenbild
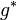 kann nicht parallel zu
kann nicht parallel zu  sein.
sein.
- Dementsprechend hat
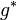 mit
mit  genau einen Punkt gemeinsam. Wir bezeichnen ihn mit
genau einen Punkt gemeinsam. Wir bezeichnen ihn mit 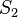 .
.
- Der Winkel zwischen
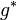 und
und  sei mit
sei mit  bezeichnet.
bezeichnet.
- Als Punkt der Geraden
 ist
ist 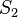 Fixpunkt bei
Fixpunkt bei 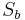 .
.
- Weil
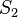 der einzige Punkt ist, den
der einzige Punkt ist, den 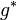 mit
mit  gemeinsam hat, ist
gemeinsam hat, ist 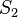 der einzige zu
der einzige zu 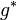 gehörige Fixpunkt bei
gehörige Fixpunkt bei 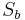 .
.
- Das Bild von
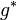 bei der Spiegelung an
bei der Spiegelung an  sei mit
sei mit 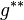 bezeichnet. Es ist identisch mit dem Bild
bezeichnet. Es ist identisch mit dem Bild 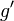 von
von  bei der Verschiebung
bei der Verschiebung 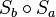 .
.
- Der Winkel zwischen
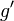 und
und  sei mit
sei mit 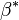 bezeichnet.
bezeichnet.
Aufgabe:
- Begründen Sie 6.
Verschiebungsweite
Satz: (über die Verschiebungsweite)
- Es sei
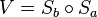 eine Verschiebung
eine Verschiebung 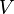 . Für jedes Paar (Originalpunkt
. Für jedes Paar (Originalpunkt  , Bildpunkt
, Bildpunkt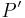 bei
bei 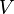 ) gilt:
) gilt: 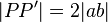 .
.
- Es sei

