Problem der Woche 12 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Entdecken Sie den Fehler:<br /> Beweis dafür, dass alle Winkel das Maß 90 haben:<br /> Vor.: Viereck <math>\overline{ABCD}</math> mit <math>\left|\angle BCD \ri…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | Entdecken Sie den Fehler:<br /> | + | '''Entdecken Sie den Fehler:'''<br /> |
Beweis dafür, dass alle Winkel das Maß 90 haben:<br /> | Beweis dafür, dass alle Winkel das Maß 90 haben:<br /> | ||
Vor.: Viereck <math>\overline{ABCD}</math> mit <math>\left|\angle BCD \right| = 90</math>; <math>\left|\angle ADC \right|\neq 90</math> und <math>\overline{BC} =\overline{AD}</math>.<br /> | Vor.: Viereck <math>\overline{ABCD}</math> mit <math>\left|\angle BCD \right| = 90</math>; <math>\left|\angle ADC \right|\neq 90</math> und <math>\overline{BC} =\overline{AD}</math>.<br /> | ||
Version vom 12. Januar 2012, 15:41 Uhr
Entdecken Sie den Fehler:
Beweis dafür, dass alle Winkel das Maß 90 haben:
Vor.: Viereck  mit
mit 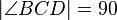 ;
; 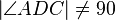 und
und 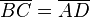 .
.
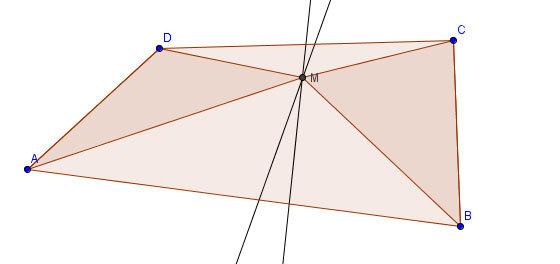
Beh.: 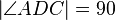
Beweis:
| Beweisschritt | Begründung |
(1) 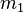 und und 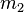 sind Mittelsenkrechten von sind Mittelsenkrechten von  und und  |
Existenz und Eindeutigkeit der Mittelsenkrechten |
(2) 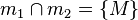 |
Genau ein Schnittpunkt von zwei nicht identischen und nicht parallelen Geraden |
(3) 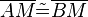 |
(1), (2), Mittelsenkrechtenkriterium |
(4) 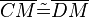 |
(1), (2), Mittelsenkrechtenkriterium |
(5) 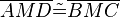 |
Vor., (3), (4), sss-Kongruenzsatz |
(6) 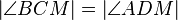 |
(5) |
(7) 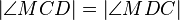 |
Basiswinkelsatz |
(8) 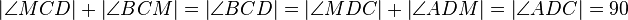 |
(6), (7), Winkeladditionsaxiom, Rechnen in R |

