Lösung der Aufgaben zur Mengenlehre (SoSe 12): Unterschied zwischen den Versionen
(→Mengenlehre) |
(→Mengenlehre) |
||
| Zeile 4: | Zeile 4: | ||
Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--[[Benutzer:Maliglowka|Maliglowka]] 16:36, 18. Apr. 2012 (CEST) | Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--[[Benutzer:Maliglowka|Maliglowka]] 16:36, 18. Apr. 2012 (CEST) | ||
| + | Die Menge A besitzt die Zahlen 1,3 und 5 auch nicht, weil sie nur gerade naatürliche Zahlen besitzt. Deswegen würde ich auch sagen, dass die Mengen identisch sind. | ||
2. <br />M1={}<br />M2={}<br />M3={-2}<br />M4={}<br />M5= <math> \sqrt{2} </math><br />M6={-2}<br /><br />M1=M2=M4<br />M3=M6--[[Benutzer:PippiLotta|PippiLotta]] 09:22, 18. Apr. 2012 (CEST)<br /> | 2. <br />M1={}<br />M2={}<br />M3={-2}<br />M4={}<br />M5= <math> \sqrt{2} </math><br />M6={-2}<br /><br />M1=M2=M4<br />M3=M6--[[Benutzer:PippiLotta|PippiLotta]] 09:22, 18. Apr. 2012 (CEST)<br /> | ||
Version vom 18. April 2012, 21:39 Uhr
Mengenlehre
1.
A und B sind identisch. --PippiLotta 09:22, 18. Apr. 2012 (CEST)
Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--Maliglowka 16:36, 18. Apr. 2012 (CEST)
Die Menge A besitzt die Zahlen 1,3 und 5 auch nicht, weil sie nur gerade naatürliche Zahlen besitzt. Deswegen würde ich auch sagen, dass die Mengen identisch sind.
2.
M1={}
M2={}
M3={-2}
M4={}
M5=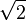 
M6={-2}
M1=M2=M4
M3=M6--PippiLotta 09:22, 18. Apr. 2012 (CEST)
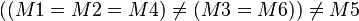--Maliglowka 16:36, 18. Apr. 2012 (CEST)
3. M1=M3 und M2 ist Teilmenge von M1/M3
4.N1=N2=N3, alles Rechtecke
Wurzelzeichen? Hier ist eins: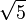
(Quelltext anschauen) Ansonsten in der Hilfe nachsehen:
Formeln_verwenden--*m.g.* 17:17, 18. Apr. 2012 (CEST)
