Übung Aufgaben 4 (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 4.5)
Zeile 1: Zeile 1:
−
=Aufgaben zum Abstand=
+
== Aufgabe 4 ==
 +
Beweisen Sie mit Hilfe einer Wahrheitstabelle:<br /><br />
  
−
==Aufgabe 4.1==
+
<math>(\ A \Rightarrow B)  \wedge (\ B \Rightarrow A)  \Leftrightarrow (\ A \Leftrightarrow B) </math><br />
−
<u>'''Satz:'''</u>
+
−
::Von drei paarweise verschiedenen Punkten <math>\ A, B</math> und <math>\ C</math> ein und derselben Geraden <math>\ g</math> liegt genau einer zwischen den beiden anderen.
+
−
Beweisen Sie diesen Satz.
+
  
−
<br />
+
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br />
−
[[Lösung von Aufgabe 4.1 (SoSe_12)]]
+
[[Lösung von Zusatzaufgabe 2.4 (SoSe_12)]]
  
−
==Aufgabe 4.2==
+
== Aufgabe 5 ==  
−
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
+
Vergleichen Sie die Wahrheitswerte von<br />
−
<math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
+
  
−
[[Tipps zu Aufgabe 4.2 (SoSe_12)]]
+
<math>(\ A \Rightarrow B) </math> und <math>(\ A  \wedge \neg B)</math>.<br />
−
<br /><br />
+
−
[[Lösung von Aufgabe 4.2 (SoSe_12)]]
+
  
−
==Aufgabe 4.3==
+
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.<br />
−
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
+
[[Lösung von Zusatzaufgabe 2.5 (SoSe_12)]]
−
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math>
+
−
 
+
−
<br />
+
−
[[Lösung von Aufgabe 4.3 (SoSe_12)]]
+
−
 
+
−
 
+
−
==Aufgabe 4.4==
+
−
Beweisen Sie: Zu jeder Strecke <math>\overline{AB} </math> existiert genau eine Strecke <math>\overline{AC} </math> auf <math>\ AB^{+} </math> mit <math>\left| AB \right| = \frac{1}{4} \left| AC \right| </math> und <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
+
−
<br />
+
−
[[Tipps zu Aufgabe 4.4 (SoSe_12)]]
+
−
<br /><br />
+
−
[[Lösung von Aufgabe 4.4 (SoSe_12)]]
+
−
 
+
−
=Weitere Aufgaben zur Inzidenz=
+
−
 
+
−
 
+
−
== Aufgabe 4.5 ==
+
−
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 3.3 und 3.5).
+
−
 
+
−
[[Lösung von Aufg. 4.5 (SoSe_12)]]
+

Version vom 19. April 2012, 09:46 Uhr

Aufgabe 4

Beweisen Sie mit Hilfe einer Wahrheitstabelle:

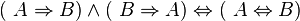
(\ A \Rightarrow B) \wedge (\ B \Rightarrow A) \Leftrightarrow (\ A \Leftrightarrow B)

Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Lösung von Zusatzaufgabe 2.4 (SoSe_12)

Aufgabe 5

Vergleichen Sie die Wahrheitswerte von

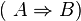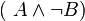(\ A \Rightarrow B) und (\ A \wedge \neg B).

Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Lösung von Zusatzaufgabe 2.5 (SoSe_12)

Von „http://geometrie.zum.de/index.php?title=Übung_Aufgaben_4_(SoSe_12)&oldid=11722“