Übung Aufgaben 2 S (SoSe 12): Unterschied zwischen den Versionen
(→Aufgabe 2.7) |
Zigzag (Diskussion | Beiträge) (→Aufgabe 2.4) |
||
| Zeile 38: | Zeile 38: | ||
<br /> | <br /> | ||
[[Lösung von Aufgabe 2.4_S (SoSe_12)]]<br /> | [[Lösung von Aufgabe 2.4_S (SoSe_12)]]<br /> | ||
| + | |||
| + | a) Wenn in einem Dreieck ABC zwei Winkel kongruent sind, dann ist dieses Dreieck ein gleichschenkliges Dreieck. | ||
| + | |||
| + | b) | ||
==Aufgabe 2.5== | ==Aufgabe 2.5== | ||
Version vom 26. April 2012, 22:38 Uhr
|
Aufgaben zu Sätzen und Beweisen Teil 1Aufgabe 2.1Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. Aufgabe 2.2a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach). Lösung von Aufgabe 2.2_S (SoSe_12)
Aufgabe 2.3Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ? Lösung von Aufgabe 2.3_S (SoSe_12) Aufgabe 2.4Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. a) Formulieren Sie den Satz mit "Wenn... dann..." b)Ergänzen Sie: a) Wenn in einem Dreieck ABC zwei Winkel kongruent sind, dann ist dieses Dreieck ein gleichschenkliges Dreieck. b) Aufgabe 2.5Eine Raute sei folgendermaßen definiert: Ein Viereck mit vier kongruenten Seiten heißt Raute. a) Formulieren Sie den Satz mit "Wenn... dann..." b)Ergänzen Sie: Aufgabe 2.6Bringen Sie die folgenden Implikationen in die Form Wenn-Dann:
Lösung von Aufgabe 2.6_S (SoSe_12) Aufgabe 2.7Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz. |
 und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?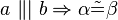
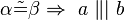
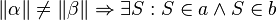
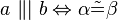
 ist ein Dreieck mit…
ist ein Dreieck mit… eindeutig bestimmt sind, sind Symmetrieachsen von
eindeutig bestimmt sind, sind Symmetrieachsen von 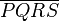 ein Paralellogramm. Es gilt:
ein Paralellogramm. Es gilt: 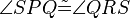 .
.

