Lösung von Aufgabe 2.4 S (SoSe 12): Unterschied zwischen den Versionen

Version vom 29. April 2012, 14:16 Uhr

$\alpha$ $\alpha$ ==Aufgabe 2.4== Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.

a) Formulieren Sie den Satz mit "Wenn... dann..."

b)Ergänzen Sie:
Voraussetzung: $\overline{ABC}$ ist ein Dreieck mit…
Behauptung:

a)Wenn ein Dreieck ABC zwei kongruente Innenwinkel hat, dann ist dieses Dreieck ein gleichschenkliches Dreieck.

b)Voraussetzung: ABC ist ein Dreieck mit zwei kongruenten Innenwinkeln. Behauptung: ABC ist ein gleichschenkliges Dreieck.

b) Vor.: $\overline {ABC}$ ist ein Dreieck mit $\overline{AC}$ = $\overline{BC}$

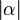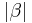Beh.: $\left| \alpha \right|$ = $\left| \beta \right|$ --Oz44oz 19:04, 27. Apr. 2012 (CEST)

Ist es bei b) nicht genau andersrum wie bei 0z44oz:

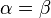
Vorraussetzung : $\alpha =\beta$

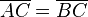
Behauptung : $\overline{AC}=\overline{BC}$

--Funkdocta 15:16, 29. Apr. 2012 (CEST)

@@ Zeile 1: / Zeile 1: @@
-==Aufgabe 2.4==
+<math>\alpha</math> <math>\alpha</math> ==Aufgabe 2.4==
 Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. <br />
@@ Zeile 25: / Zeile 25: @@
 Beh.: <math>\left| \alpha \right|</math> = <math>\left| \beta \right|</math> --[[Benutzer:Oz44oz|Oz44oz]] 19:04, 27. Apr. 2012 (CEST)
+Ist es bei b) nicht genau andersrum wie bei 0z44oz:
+Vorraussetzung : <math>\alpha =\beta</math>
+Behauptung :<math>\overline{AC}=\overline{BC} </math>
+--[[Benutzer:Funkdocta|Funkdocta]] 15:16, 29. Apr. 2012 (CEST)