Lösung von Aufgabe 3.5 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „==Aufgabe 3.5== Gegeben sei folgende Äquivalenz: Der Abstand zweier Punkte ''A'' und ''B'' ist genau dann 0, wenn ''A'' und ''B'' identisch sind.<br /> a) Formul…“) |
(→Aufgabe 3.5) |
||
| Zeile 1: | Zeile 1: | ||
==Aufgabe 3.5== | ==Aufgabe 3.5== | ||
| − | + | Das Parallelenaxiom lautet wie folgt:<br /> | |
| − | + | Zu jeder Geraden ''g'' und zu jedem nicht auf ''g'' liegenden Punkt ''A'' gibt es höchstens eine Gerade, die durch ''A'' verläuft und zu ''g'' parallel ist.<br /> | |
| − | b | + | Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:<br /> |
| − | + | Es seien ''a'', ''b'' und ''c'' drei paarweise verschiedene Geraden in ein und derselben Ebene.<br /> | |
| + | a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: <math>\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c</math> . <br /> | ||
| + | b) Welche Eigenschaft der Relation <math>\|| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br /> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Version vom 30. April 2012, 12:56 Uhr
Aufgabe 3.5
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 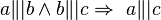 .
.
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?

