Lösung von Aufgabe 3.1 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösungsvorschlag 3:)
(→‎Lösungsvorschlag 3:)
Zeile 26: Zeile 26:
  
 
Aber im zweiten Vorschlag könnte es doch auch sein, dass die Mittelsenkrechte die Strecke in jedem beliebigen Winkel schneidet, oder?
 
Aber im zweiten Vorschlag könnte es doch auch sein, dass die Mittelsenkrechte die Strecke in jedem beliebigen Winkel schneidet, oder?
 +
 +
===Kommentar M.G.===
 +
@Hauleri Sie wollen den Begriff ''Mittelsenkrechte'' in ''Wenn-Dann-Form'' definieren. Ich bring hier mal ein paar andere Konventionaldefinitionen:
 +
{{Definition|Es seien ''t'' und  <math>a</math> zwei ganze Zahlen. Wenn es eine ganze Zahl <math>n</math> derart gibt, dass <math>t \cdot n = a</math> gilt, dann ist <math>t</math> ein ''Teiler'' von <math>a</math>.}}

Version vom 6. Mai 2012, 16:41 Uhr

Inhaltsverzeichnis

Aufgabe 3.1

Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.


Wenn eine Gerade g senkrecht auf einer Strecke \overline{AB} steht und durch den Mittelpunkt der Strecke \overline{AB} verläuft, dann ist g Mittelsenkrechte.--Oz44oz 21:53, 1. Mai 2012 (CEST)

Lösungsvorschlag 2:

Wenn eine Gerade eine Mittelsenkrechte ist, dann halbiert sie eine Strecke \overline{AB} und steht dabei senkrecht auf ihr.

Da hier ja nach zwei prinzipiell verchiedenen Konventionaldefinitionen gefragt ist. Meine Frage: Könnte man auch folgendes sagen?????

Wenn eine Gerade eine Mittelsenkrechte ist, dann ist sie die Menge aller Punkte, die von zwei Punkten A und B den gleichen Abstand hat.

Ansonsten fallen mir nämlich nurnoch ähnliche Forumlierungen wie oben ein.--Goliath 17:42, 3. Mai 2012 (CEST)


Lösungsvorschlag 3:

Wenn eine Mittelsenkrechte auf die Strecke \overline{AB} trifft, dann sind die beiden Nebenwinkel rechte Winkel.

Wenn eine Mittelsenkrechte die Strecke \overline{AB} schneidet, dann ist der Schnittpunkt der Mittelpunkt M der Geraden \overline{AB} . --Hauleri 13:10, 6. Mai 2012 (CEST)

Aber im zweiten Vorschlag könnte es doch auch sein, dass die Mittelsenkrechte die Strecke in jedem beliebigen Winkel schneidet, oder?

Kommentar M.G.

@Hauleri Sie wollen den Begriff Mittelsenkrechte in Wenn-Dann-Form definieren. Ich bring hier mal ein paar andere Konventionaldefinitionen:

Definition

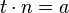Es seien t und a zwei ganze Zahlen. Wenn es eine ganze Zahl n derart gibt, dass t \cdot n = a gilt, dann ist t ein Teiler von a.

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_3.1_S_(SoSe_12)&oldid=12874“