Lösung von Aufgabe 4.2P (SoSe 12): Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
transitiv : gRh und hRc <math>\Rightarrow</math> gRc | transitiv : gRh und hRc <math>\Rightarrow</math> gRc | ||
| − | somit gRh stimmt ja somit | + | somit gRh stimmt ja somit ist die Aussage wahr und hRc geht nicht, da kein c definiert ist, somit ist hRc falsch. Alles in allem ist die wahre Aussage und falsche Aussage immer eine falsche Aussage (UND-Aussage). Und durch die Implikation ist es egal was hinten raus kommt die Aussage ist wahr (<math>\Rightarrow</math> Aussage). Hoffe konnte es verständlich ausführen.--[[Benutzer:Malilglowka|Malilglowka]] 23:41, 10. Mai 2012 (CEST) |
Version vom 10. Mai 2012, 22:42 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
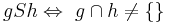
Reflexiv, symmetrisch und transitiv  Äquivalenzrelation --Malilglowka 17:29, 10. Mai 2012 (CEST)
Äquivalenzrelation --Malilglowka 17:29, 10. Mai 2012 (CEST)
reflexiv: würde ich zustimmen, denn eine menge mit sich selbst geschnitten keine leere menge ergibt
symmetrisch: ja, weil das kommutativgesetz gilt (auch g und h haben keine leere menge.
transitiv: würde ich dir nicht zustimmen: wenn g geschnitten mit h keine leere menge hat und h mit i geschnitten keine leere menge, können wir nichts darüber aussagen, ob g und i geschnitten nicht doch eine leere menge haben
- zahlenbeispiel: wenn 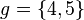 und
und 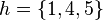 und
und 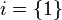 , dann haben g geschnitten mit i eine leere menge.
, dann haben g geschnitten mit i eine leere menge.
- beispiel aus der geometrie: wenn g eine gerade ist und h schneidet g, dann hätte i, wenn sie zu g parallel ist, zwar auch einen punkt mit h gemeinsam, aber nicht zur parallelen geraden g--Studentin 19:21, 10. Mai 2012 (CEST)
transitiv : gRh und hRc  gRc
somit gRh stimmt ja somit ist die Aussage wahr und hRc geht nicht, da kein c definiert ist, somit ist hRc falsch. Alles in allem ist die wahre Aussage und falsche Aussage immer eine falsche Aussage (UND-Aussage). Und durch die Implikation ist es egal was hinten raus kommt die Aussage ist wahr (
gRc
somit gRh stimmt ja somit ist die Aussage wahr und hRc geht nicht, da kein c definiert ist, somit ist hRc falsch. Alles in allem ist die wahre Aussage und falsche Aussage immer eine falsche Aussage (UND-Aussage). Und durch die Implikation ist es egal was hinten raus kommt die Aussage ist wahr ( Aussage). Hoffe konnte es verständlich ausführen.--Malilglowka 23:41, 10. Mai 2012 (CEST)
Aussage). Hoffe konnte es verständlich ausführen.--Malilglowka 23:41, 10. Mai 2012 (CEST)

