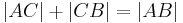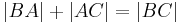Aus der Vorlesung vom 15.05.2012: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „= Der Abstand zweier Punkte = === Die ersten beiden Abstandsaxiome === ===== Axiom II.1: (Abstandsaxiom) ===== :Zu je zwei Punkten <math>\ A</math> und <math>\ …“) |
K |
||
| Zeile 1: | Zeile 1: | ||
| + | == Aufgabe == | ||
| + | |||
| + | Wir teilen den Vorlesungsraum in '''4 Gruppen''':<br /> | ||
| + | Gruppe "Fenster", Gruppe "Mitte Nähe Fenster", Gruppe "Mitte Nähe Wand", Gruppe "Wand".<br /><br /> | ||
| + | |||
| + | '''Bitte definieren Sie...'''<br /> | ||
| + | |||
| + | * Gruppe '''Fenster: "parallel auf der Menge der Geraden"''' | ||
| + | * Gruppe '''Mitte Nähe Fenster: "parallel auf der Menge der Ebenen"''' | ||
| + | * Gruppe '''Mitte Nähe Wand: "windschief auf der Menge der Geraden"''' | ||
| + | * Gruppe '''Wand: "windschief auf der Menge der Ebenen"''' | ||
| + | <br /> | ||
| + | Berabeitungszeit: 3 Minuten. Los geht´s! | ||
| + | |||
| + | |||
= Der Abstand zweier Punkte = | = Der Abstand zweier Punkte = | ||
=== Die ersten beiden Abstandsaxiome === | === Die ersten beiden Abstandsaxiome === | ||
Version vom 15. Mai 2012, 13:06 Uhr
Inhaltsverzeichnis |
Aufgabe
Wir teilen den Vorlesungsraum in 4 Gruppen:
Gruppe "Fenster", Gruppe "Mitte Nähe Fenster", Gruppe "Mitte Nähe Wand", Gruppe "Wand".
Bitte definieren Sie...
- Gruppe Fenster: "parallel auf der Menge der Geraden"
- Gruppe Mitte Nähe Fenster: "parallel auf der Menge der Ebenen"
- Gruppe Mitte Nähe Wand: "windschief auf der Menge der Geraden"
- Gruppe Wand: "windschief auf der Menge der Ebenen"
Berabeitungszeit: 3 Minuten. Los geht´s!
Der Abstand zweier Punkte
Die ersten beiden Abstandsaxiome
Axiom II.1: (Abstandsaxiom)
- Zu je zwei Punkten
 und
und  gibt es eine eindeutig bestimmte nicht negative reelle Zahl
gibt es eine eindeutig bestimmte nicht negative reelle Zahl 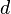 mit
mit 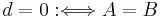 .
.
Definition II.1: (Abstand)
- Der Abstand zweier Punkte
 und
und  ist die Zahl, die nach dem Abstandsaxiom den Punkten
ist die Zahl, die nach dem Abstandsaxiom den Punkten  und
und  zugeordnet werden kann.
zugeordnet werden kann.
Schreibweise: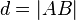 .
.
Axiom II.2:
- Für zwei beliebige Punkte
 und
und  gilt
gilt 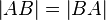 .
.
Aufgabe
Konstruieren Sie jeweils die drei Punkte  und
und  für die gilt:
für die gilt:
a)  = 4,
= 4, 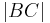 = 3,
= 3, 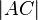 = 5
= 5
b)  = 2,
= 2, 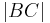 = 3,
= 3, 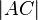 = 5
= 5
c)  = 1,
= 1, 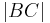 = 2,
= 2, 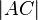 = 5
= 5
Das Axiom der Dreiecksungleichung
Axiom II/3: (Dreiecksungleichung)
- Für drei beliebige Punkte
 und
und  gilt:
gilt: 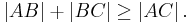
- Für drei beliebige Punkte
- Falls
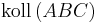 , dann ist eine der folgenden Gleichungen erfüllt:
, dann ist eine der folgenden Gleichungen erfüllt:
- Falls
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
 ,
,  und
und  kollinear.
kollinear.
Definitionen und Sätze
Definition II.2: (Zwischenrelation)
- Ein Punkt
 liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn gilt:
, wenn gilt:
- Ein Punkt
-
 und
und
 ,
,  und
und  sind paarweise verschieden.
sind paarweise verschieden.
-
- Schreibweise:

- Schreibweise:
Es gelten die folgenden Sätze:
Satz II.1
- Aus
 folgt
folgt 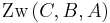 .
.
- Aus
Satz II.2:
- Aus
 folgt
folgt  .
.
- Aus
Satz II.3
- Es sei
 mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt genau eine der Zwischenrelationen, d.h. entweder oder
oder 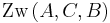 oder
oder 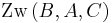 .
.
- Es sei
Beweis von Satz II.3:
Übungsaufgabe (5.1). Beweisideen?
Strecken und Halbgeraden
Aufgabe
Definieren Sie:
Definition II.3: (Strecke, Endpunkte einer Strecke)
- Es seien
 und
und  zwei verschiedene Punkte. ... (ergänzen Sie)
zwei verschiedene Punkte. ... (ergänzen Sie)
- Es seien
Definition II.4: (Länge einer Strecke)
- Es seien
 und
und  zwei verschiedene Punkte. ... (ergänzen Sie)
zwei verschiedene Punkte. ... (ergänzen Sie)
- Es seien
Definition II.5: (Halbgerade, bzw. Strahl)
- Definition (Halbgerade
 ): ......(ergänzen Sie)
): ......(ergänzen Sie)
- Definition (Halbgerade
 ): ......(ergänzen Sie)
): ......(ergänzen Sie)
- Definition (Halbgerade