Lösung von Zusatzaufgabe 5.2 P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie: Ist ''O'' ein beliebiger Punkt einer Geraden ''g'' und ''A'' ein weiterer (von ''O'' verschiedener) Punkt dieser Geraden, so gilt für die Halbgerad…“) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Ist ''O'' ein beliebiger Punkt einer Geraden ''g'' und ''A'' ein weiterer (von ''O'' verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden <math>\ OA^{+}</math> und <math>\ OA^{-}</math> :<br /> | Beweisen Sie: Ist ''O'' ein beliebiger Punkt einer Geraden ''g'' und ''A'' ein weiterer (von ''O'' verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden <math>\ OA^{+}</math> und <math>\ OA^{-}</math> :<br /> | ||
a)<math>\ OA^{+} \cap \ OA^{-}=\{O\} </math> und<br /> | a)<math>\ OA^{+} \cap \ OA^{-}=\{O\} </math> und<br /> | ||
| − | b)<math>\ OA^{+} \cup \ OA^{-}=g </math> | + | b)<math>\ OA^{+} \cup \ OA^{-}=g </math><br /><br /> |
| + | |||
| + | a)<math>\ OA^{+} \cap \ OA^{-}=\{O\} </math><br /><br /> | ||
| + | |||
| + | <math>\ OA^{+}= \{P|(Zw) (O, P, A)\} \cup \{P|(Zw) (O, A, P)\} \cup \{O\} \cup \{A\}</math> <br /> | ||
| + | <math>\ OA^{-}= \{P|(Zw) (P, O, A)\} \cup \{O\} </math> <br /> | ||
| + | in der schnittmenge gibt es nur ein gemeinsames element: "o" <br /><br /> | ||
| + | |||
| + | b)<math>\ OA^{+} \cup \ OA^{-}=g </math><br /><br /> | ||
| + | |||
| + | <math>\ OA^{+}= \{P|(Zw) (O, P, A)\} \cup \{P|(Zw) (O, A, P)\} \cup \{O\} \cup \{A\}</math> <br /> | ||
| + | <math>\ OA^{-}= \{P|(Zw) (P, O, A)\} \cup \{O\} </math> <br /> | ||
| + | in der vereinigungsmenge ist die gerade g, da in der vereinigungsmenge sowohl die punkte a und o, als auch alle punkte zw (a,o,p), zw (p,o,a), zw (o,p,a) enthalten sind.<br /> | ||
| + | --[[Benutzer:Studentin|Studentin]] 16:35, 27. Mai 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 27. Mai 2012, 15:35 Uhr
Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden 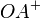 und
und 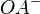 :
:
a)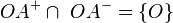 und
und
b)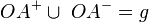
a)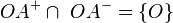
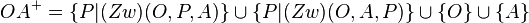
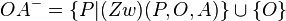
in der schnittmenge gibt es nur ein gemeinsames element: "o"
b)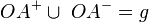
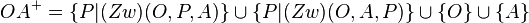
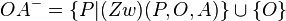
in der vereinigungsmenge ist die gerade g, da in der vereinigungsmenge sowohl die punkte a und o, als auch alle punkte zw (a,o,p), zw (p,o,a), zw (o,p,a) enthalten sind.
--Studentin 16:35, 27. Mai 2012 (CEST)

