Lösung von Aufgabe 5.3 S (SoSe 12): Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
| + | |||
| + | |||
| + | |||
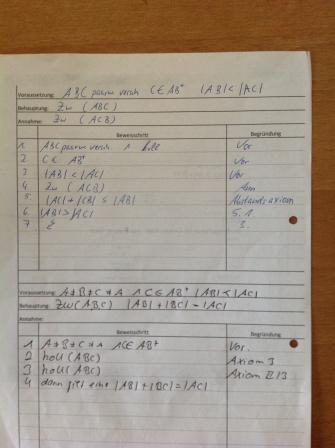
| + | {| class="wikitable sortable" | ||
| + | !Was mache ich!!Warum darf ich das? | ||
| + | |- | ||
| + | | C Element ABplus || Voraussetzung | ||
| + | |- | ||
| + | | koll(A,B,C) || (1) | ||
| + | |- | ||
| + | | |AB| + |BC| = |AC| <br/ > || Zwischenrelation, (2) | ||
| + | |BC| + |CA| = |BA| <br/ > | ||
| + | |BA| + |AC| = |BC| | ||
| + | |- | ||
| + | | Zw(A,B,C) v Zw(A,C,B) v Zw(B,A,C) || Zwischenrelation, (3) | ||
| + | |} | ||
| + | <br/> | ||
| + | Nun ist gezeigt, dass eine der Zwischenrelationen gilt (Existenz). <br/ > | ||
| + | Frage: Habe ich zwei Möglichkeiten? <br/ > | ||
| + | 1.: <br/> | ||
| + | Ich zeige, dass Zw(B,A,C) (1. Annahme) und dass Zw(A,C,B) (2. Annahme) nicht gilt. <br/ > | ||
| + | 2.: <br/ > | ||
| + | Ich zeige, dass zwei Zwischenrelationen nicht gelten. <br/ > | ||
| + | Ich bin der Meinung, dass die erste Möglichkeit als einzige möglich sein müsste, weil wir ja konkret beweise müssen, dass B zwischen A und C liegt.<br/ > | ||
| + | Oder muss ich beide Annahmen zum Widerspruch führen? <br/ > | ||
| + | --[[Benutzer:RitterSport|RitterSport]] 15:01, 30. Mai 2012 (CEST) | ||
Version vom 30. Mai 2012, 14:01 Uhr
Zeigen Sie, dass für drei paarweise verschiedene Punkte 
und 
gilt:
Wenn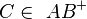 
und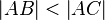 
dann gilt 
ich habe Schwierigkeiten das Plus beim B zu interpretieren. Ist Zw. (ABC) eine fertige Aussage?--KeinKurpfälzer 17:09, 21. Mai 2012 (CEST)
Gut, dass Sie fragen.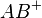 
ist die Halbgerade, die bei A beginnt und in Richtung B verläuft. Werden wir am Donnerstag behandeln. Und Ihre zweite Frage: Ja, ist eine fertige Aussage. In Worten: B liegt zwischen A und C.--Buchner 10:28, 22. Mai 2012 (CEST)
--H2O 18:58, 21. Mai 2012 (CEST)
| Was mache ich | Warum darf ich das? | ||
|---|---|---|---|
| C Element ABplus | Voraussetzung | ||
| koll(A,B,C) | (1) | ||
| AB| + |BC| = |AC| |
Zwischenrelation, (2) | + |CA| = |BA| |
+ |AC| = |BC| |
| Zw(A,B,C) v Zw(A,C,B) v Zw(B,A,C) | Zwischenrelation, (3) |
Nun ist gezeigt, dass eine der Zwischenrelationen gilt (Existenz).
Frage: Habe ich zwei Möglichkeiten?
1.:
Ich zeige, dass Zw(B,A,C) (1. Annahme) und dass Zw(A,C,B) (2. Annahme) nicht gilt.
2.:
Ich zeige, dass zwei Zwischenrelationen nicht gelten.
Ich bin der Meinung, dass die erste Möglichkeit als einzige möglich sein müsste, weil wir ja konkret beweise müssen, dass B zwischen A und C liegt.
Oder muss ich beide Annahmen zum Widerspruch führen?
--RitterSport 15:01, 30. Mai 2012 (CEST)
