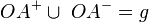Zusatz 7 (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
| − | == | + | == Zusatzaufgabe 7.1 == |
Gegeben sei ein Dreieck <math>\overline{ABC} </math> und eine Gerade g.<br /> | Gegeben sei ein Dreieck <math>\overline{ABC} </math> und eine Gerade g.<br /> | ||
Behauptung: Wenn g eine Seite von <math>\overline{ABC} </math> schneidet, dann schneidet g genau eine weitere Seite von <math>\overline{ABC} </math>.<br /><br /> | Behauptung: Wenn g eine Seite von <math>\overline{ABC} </math> schneidet, dann schneidet g genau eine weitere Seite von <math>\overline{ABC} </math>.<br /><br /> | ||
'''a)''' Vergleichen Sie diese Behauptung mit dem Axiom von Pasch. Wo liegt der Unterschied?<br /> | '''a)''' Vergleichen Sie diese Behauptung mit dem Axiom von Pasch. Wo liegt der Unterschied?<br /> | ||
'''b)''' Widerlegen Sie die Behauptung durch eine Skizze.<br /> | '''b)''' Widerlegen Sie die Behauptung durch eine Skizze.<br /> | ||
| − | [[Lösung von | + | [[Lösung von Zusatzaufgabe 7.1_S (SoSe_12)]] |
<br /> | <br /> | ||
| − | == | + | == Zusatzaufgabe 7.2 == |
Die grauen Flächen seien Punktmengen (Teilmengen einer Ebene). Welche Figuren sind konvex? Warum (nicht)?<br /> | Die grauen Flächen seien Punktmengen (Teilmengen einer Ebene). Welche Figuren sind konvex? Warum (nicht)?<br /> | ||
[[Bild:konvex01.gif|links]]<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> | [[Bild:konvex01.gif|links]]<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> | ||
| − | [[Lösung von | + | [[Lösung von Zusatzaufgabe 7.2_S (SoSe_12)]] |
<br /> | <br /> | ||
| − | == | + | == Zusatzaufgabe 7.3 == |
Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden <math>\ OA^{+} </math> und <math>\ OA^{-} </math> :<br /> | Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden <math>\ OA^{+} </math> und <math>\ OA^{-} </math> :<br /> | ||
a) <math>\ OA^{+} \cap \ OA^{-} = \{O\} </math> <br /> | a) <math>\ OA^{+} \cap \ OA^{-} = \{O\} </math> <br /> | ||
b) <math>\ OA^{+} \cup \ OA^{-} = g </math> | b) <math>\ OA^{+} \cup \ OA^{-} = g </math> | ||
| − | [[Lösung von | + | [[Lösung von Zusatzaufgabe 7.3_S]] |
Aktuelle Version vom 31. Mai 2012, 16:03 Uhr
Zusatzaufgabe 7.1
Gegeben sei ein Dreieck 
und eine Gerade g.
Behauptung: Wenn g eine Seite von schneidet, dann schneidet g genau eine weitere Seite von .
a) Vergleichen Sie diese Behauptung mit dem Axiom von Pasch. Wo liegt der Unterschied?
b) Widerlegen Sie die Behauptung durch eine Skizze.
Lösung von Zusatzaufgabe 7.1_S (SoSe_12)
Zusatzaufgabe 7.2
Die grauen Flächen seien Punktmengen (Teilmengen einer Ebene). Welche Figuren sind konvex? Warum (nicht)?
Lösung von Zusatzaufgabe 7.2_S (SoSe_12)
Zusatzaufgabe 7.3
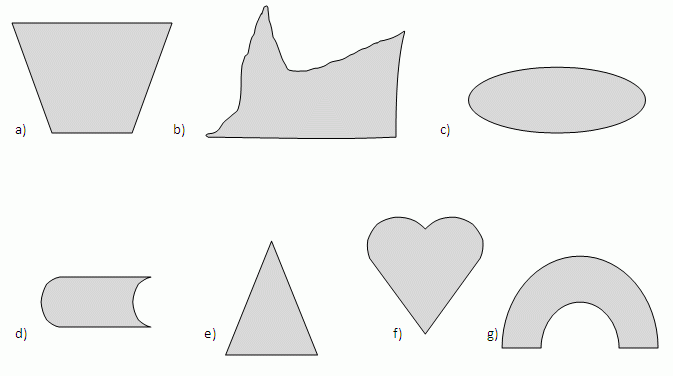
Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden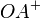 
und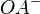 
:
a)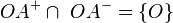 
b) 
