Zusatzaufgaben 6 P (SoSe 12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „==Zusatzaufgabe 6.1== Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser ei…“) |
(→Zusatzaufgabe 6.2) |
||
| Zeile 12: | Zeile 12: | ||
c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.<br /> | c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.<br /> | ||
| − | [[Lösung von | + | [[Lösung von zusatzAufgabe 6.2P (SoSe_12)]] |
| − | + | ||
== Zusatzaufgabe 6.3 == | == Zusatzaufgabe 6.3 == | ||
Version vom 3. Juni 2012, 15:57 Uhr
Inhaltsverzeichnis |
Zusatzaufgabe 6.1
Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.
Lösung von Zusatzaufgabe 6.1P (SoSe_12)
Zusatzaufgabe 6.2
a) Definieren Sie den Begriff: "Konkave Punktmenge" ohne den Begriff "konvex" zu gebrauchen.
b) Begründen Sie, dass der Schnitt einer offenen Halbebene E mit einer Halbgeraden, die zwei Punkte mit E gemeinsam hat, auf jeden Fall eine konvexe Punktmenge ist.
c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.
Lösung von zusatzAufgabe 6.2P (SoSe_12)
Zusatzaufgabe 6.3
Definieren Sie noch einmal die Begriffe Halbgerade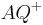 
und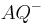 
. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden.
Lösung von Zusatzaufgabe 6.3P (SoSe_12)
Zusatzaufgabe 6.4
Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreieckschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet.
Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage.
Lösung von Zusatzaufgabe 6.4P (SoSe_12)
