Lösung von Aufgabe 6.1 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 6.1)
(→‎Aufgabe 6.1)
Zeile 12: Zeile 12:
 
Es seien A und B zwei verschiedene Punkte. Wenn man die Strecke AB und alle Punkte P, die mit AB kollinear sind und von B aus hinter A liegen vereinigt, dann erhält man die Halbgerade AB-.<br />
 
Es seien A und B zwei verschiedene Punkte. Wenn man die Strecke AB und alle Punkte P, die mit AB kollinear sind und von B aus hinter A liegen vereinigt, dann erhält man die Halbgerade AB-.<br />
 
--[[Benutzer:Monsta|Monsta]] 22:41, 4. Jun. 2012 (CEST)
 
--[[Benutzer:Monsta|Monsta]] 22:41, 4. Jun. 2012 (CEST)
 +
 +
 +
=== Anmerkungen von Buchner zu Monstas Definitionen ===
 +
Zur Definition Strecke: Die Definition ist korrekt- allerdings brauchen Sie die Gerade g nicht zu nennen. Die Zwischenrealtion beinhaltet schon, dass alle Punkte kollinear sein müssen.<br />
 +
Zur Definition <math>\ AB^{+} </math>: Von der Idee absolut richtig. Allerdings ist "hinter B liegen" informell. Versuchen Sie es mal mit der Zwischenrealtion auszudrücken!<br />
 +
Zur Definition <math>\ AB^{-} </math>: Achtung: Strecke <math>\overline{AB} </math> gehört nicht dazu!<br /><br />
 +
--[[Benutzer:Buchner|Buchner]] 12:20, 6. Jun. 2012 (CEST)

Version vom 6. Juni 2012, 11:20 Uhr

Aufgabe 6.1

Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade AB^+ und die Halbgerade AB^-. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)

Strecke:
Es seien A und B zwei verschiedene Punkte auf einer Geraden g. Alle Punkte die auf dieser Geraden zwischen A und B liegen, zusammen mit den beiden Punkten selbst, bilden die Strecke AB.
Halbgerade AB+
Es seien A und B zwei verschiedene Punkte. Wenn man die Strecke AB und alle Punkte P, die mit AB kollinear sind und von A aus hinter B liegen vereinigt, dann erhält man die Halbgerade AB+.
Halbgerade AB-
Es seien A und B zwei verschiedene Punkte. Wenn man die Strecke AB und alle Punkte P, die mit AB kollinear sind und von B aus hinter A liegen vereinigt, dann erhält man die Halbgerade AB-.
--Monsta 22:41, 4. Jun. 2012 (CEST)


Anmerkungen von Buchner zu Monstas Definitionen

Zur Definition Strecke: Die Definition ist korrekt- allerdings brauchen Sie die Gerade g nicht zu nennen. Die Zwischenrealtion beinhaltet schon, dass alle Punkte kollinear sein müssen.
Zur Definition \ AB^{+} : Von der Idee absolut richtig. Allerdings ist "hinter B liegen" informell. Versuchen Sie es mal mit der Zwischenrealtion auszudrücken!
Zur Definition 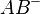\ AB^{-} : Achtung: Strecke \overline{AB} gehört nicht dazu!

--Buchner 12:20, 6. Jun. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_6.1_S_(SoSe_12)&oldid=14261“