Benutzer:*m.g.*: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen) |
*m.g.* (Diskussion | Beiträge) (→Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen) |
||
| Zeile 71: | Zeile 71: | ||
|- | |- | ||
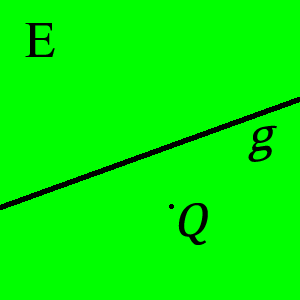
| Zu unsere Vorstellung von der Eigenschaften einer beliebigen Ebene <math>\Epsilon</math> gehört u.a., dass jede Gerade <math>\ g</math>, die zu unserer jeweiligen Ebene <math>\Epsilon</math> gehört, diese in zwei ''Hälften'' bzw. zwei ''Seiten'' einteilt. Zur Kennzeichnung der beiden ''Seiten'' von <math>\Epsilon</math> bezüglich der Geraden <math>\ g</math> verwenden wir einen Punkt <math>\ Q \in \Epsilon</math>, welcher nicht zu <math>\ g</math> gehören sollte. | | Zu unsere Vorstellung von der Eigenschaften einer beliebigen Ebene <math>\Epsilon</math> gehört u.a., dass jede Gerade <math>\ g</math>, die zu unserer jeweiligen Ebene <math>\Epsilon</math> gehört, diese in zwei ''Hälften'' bzw. zwei ''Seiten'' einteilt. Zur Kennzeichnung der beiden ''Seiten'' von <math>\Epsilon</math> bezüglich der Geraden <math>\ g</math> verwenden wir einen Punkt <math>\ Q \in \Epsilon</math>, welcher nicht zu <math>\ g</math> gehören sollte. | ||
| − | | | + | |[[Bild:Halbebene_00.png]] |
|- | |- | ||
| Element | | Element | ||
| Element | | Element | ||
|} | |} | ||
Version vom 3. Juni 2010, 08:02 Uhr
Inhaltsverzeichnis |
Halbebenen und das Axiom von Pasch
Halbebenen
Analogiebetrachtungen
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |
 ist eine ... ist eine ...
|
 ist eine ... ist eine ...
|
 | |
| Dimension von | Dimension von |
 , das , das  in Klassen einteilt in Klassen einteilt | |
 ist ... ist ...
|
 ist ... ist ...
|
 | |
 hat die Dimension ... hat die Dimension ...
|
 hat die Dimension ... hat die Dimension ...
|
 teilt teilt 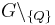 in genau zwei Klassen in genau zwei Klassen | |
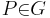 , die mit , die mit  bezüglich bezüglich  „auf derselben Seite liegen“ „auf derselben Seite liegen“ | |
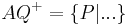
|
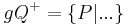
|
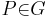 , die bezüglich , die bezüglich  nicht auf der Seite von nicht auf der Seite von  liegen. liegen. | |
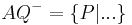
|
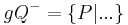
|
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade  , die zu unserer jeweiligen Ebene
, die zu unserer jeweiligen Ebene 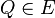 , welcher nicht zu
, welcher nicht zu