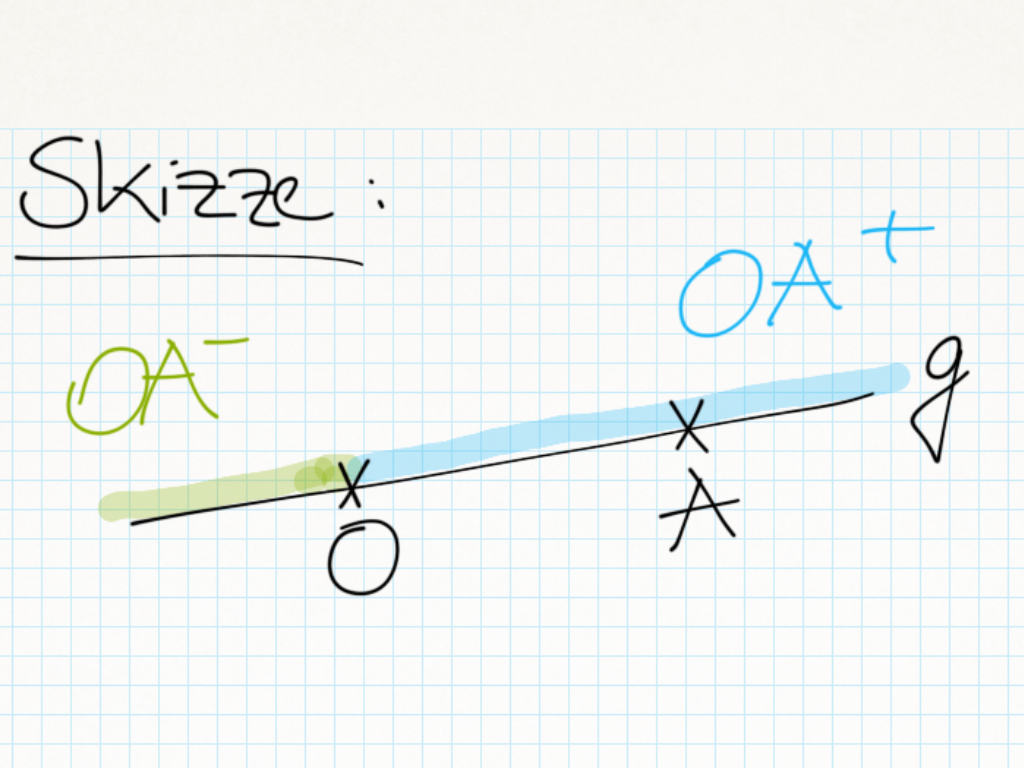Lösung von Zusatzaufgabe 7.3 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Thommy (Diskussion | Beiträge) |
Thommy (Diskussion | Beiträge) |
||
| Zeile 10: | Zeile 10: | ||
Schritt 2:<math>\ OA^{-} := \left\{ {P|\operatorname(Zw) (P, O, A) } \right\} \cup\left\{ {O} \right\}</math> <br /> | Schritt 2:<math>\ OA^{-} := \left\{ {P|\operatorname(Zw) (P, O, A) } \right\} \cup\left\{ {O} \right\}</math> <br /> | ||
Schritt 1 und 2 jeweils aufgrund der Definition II.5 (Halbgerade, bzw. Strahl) <br /> | Schritt 1 und 2 jeweils aufgrund der Definition II.5 (Halbgerade, bzw. Strahl) <br /> | ||
| + | |||
| + | Schritt 3: <math>OA^+ \cap OA^-=\left\{ {0} \right\}</math> aufgrund von (1) und (2)<br /> | ||
| + | |||
| + | Ist dies schon ausreichend? Muss noch genau gezeigt werden, dass kein weiterer Punkt P in der Schnittmenge auftritt oder ist dies durch die Zwischenrelationen schon drin?<br />--[[Benutzer:Thommy|Thommy]] 16:53, 14. Jun. 2012 (CEST) | ||
Version vom 14. Juni 2012, 15:53 Uhr
Beweis folgt..
--Tchu Tcha Tcha 20:18, 12. Jun. 2012 (CEST)
Vorraussetzung: 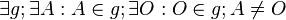
Behauptung: 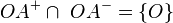
Ich möchte zunächst zeigen welche Punkte zur Halbgeraden 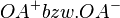 gehören:
gehören:
Schritt 1: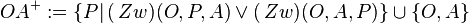
Schritt 2: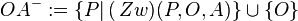
Schritt 1 und 2 jeweils aufgrund der Definition II.5 (Halbgerade, bzw. Strahl)
Schritt 3: 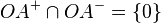 aufgrund von (1) und (2)
aufgrund von (1) und (2)
Ist dies schon ausreichend? Muss noch genau gezeigt werden, dass kein weiterer Punkt P in der Schnittmenge auftritt oder ist dies durch die Zwischenrelationen schon drin?
--Thommy 16:53, 14. Jun. 2012 (CEST)