DefinitionsversucheV4: Unterschied zwischen den Versionen
(→Variante 2) |
K (→Bemerkung Buchner) |
||
| Zeile 26: | Zeile 26: | ||
Gut, so in der Art ist es korrekt. Sie haben noch ein bisschen zu viel drin: dass die Scheitelpunkte identisch sind können sie weglassen, das ergibt sich automatisch, wenn ein Schenkel identisch ist. Ihre Idee mit "genau ein" ist inhaltlich wirklich gut. Sprachlich wirds bisschen einfacher, wenn Sie schreiben, dass die beiden anderen Schenkel eine Gerade ''bilden'' (antelle von Teilmenge), das schließt dann aus, dass die anderen beiden Schenkel auch identisch sind. Dann können Sie ''jeweils genau ein'' weglassen und es klingt sprachlich etwas glatter.<br /> | Gut, so in der Art ist es korrekt. Sie haben noch ein bisschen zu viel drin: dass die Scheitelpunkte identisch sind können sie weglassen, das ergibt sich automatisch, wenn ein Schenkel identisch ist. Ihre Idee mit "genau ein" ist inhaltlich wirklich gut. Sprachlich wirds bisschen einfacher, wenn Sie schreiben, dass die beiden anderen Schenkel eine Gerade ''bilden'' (antelle von Teilmenge), das schließt dann aus, dass die anderen beiden Schenkel auch identisch sind. Dann können Sie ''jeweils genau ein'' weglassen und es klingt sprachlich etwas glatter.<br /> | ||
<br /> | <br /> | ||
| − | '''Zu Variante | + | '''Zu Variante 2a von Nummero6/TchuTcha Tcha'''<br /> |
Gut, nur ein Tippfehler: Statt "für die Schenkel gilt" meinten Sie sicher "für die Winkel gilt".<br /> | Gut, nur ein Tippfehler: Statt "für die Schenkel gilt" meinten Sie sicher "für die Winkel gilt".<br /> | ||
--[[Benutzer:Buchner|Buchner]] 10:47, 17. Jun. 2012 (CEST)<br /> | --[[Benutzer:Buchner|Buchner]] 10:47, 17. Jun. 2012 (CEST)<br /> | ||
Version vom 17. Juni 2012, 11:33 Uhr
Inhaltsverzeichnis |
Die Vorgabe
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn ...
Definition von osterhase
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn sie supplementär sind/sich zu 180 Grad ergänzen.
--*osterhase* 19:29, 10. Jun. 2012 (CEST)
Bemerkung M.G.
s. Bemerkung zur Definition von Snooth
Definition von Nummero6/TchuTcha Tcha
Variante 1a
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn beide Scheitelpunkte identisch sind, jeweils genau ein Schenkel identisch ist und die beiden anderen Schenkel jeweils Teilmenge von genau einer Geraden sind.
Variante 2a
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn nkoll (A,S,B) und für die beiden Schenkel gilt:
- Winkel 1:
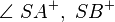
- Winkel 2:
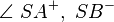
- Winkel 1:
--Tchu Tcha Tcha 21:04, 10. Jun. 2012 (CEST)
Bemerkung Buchner
Zu Variante 1a von Nummero6/TchuTcha Tcha
Gut, so in der Art ist es korrekt. Sie haben noch ein bisschen zu viel drin: dass die Scheitelpunkte identisch sind können sie weglassen, das ergibt sich automatisch, wenn ein Schenkel identisch ist. Ihre Idee mit "genau ein" ist inhaltlich wirklich gut. Sprachlich wirds bisschen einfacher, wenn Sie schreiben, dass die beiden anderen Schenkel eine Gerade bilden (antelle von Teilmenge), das schließt dann aus, dass die anderen beiden Schenkel auch identisch sind. Dann können Sie jeweils genau ein weglassen und es klingt sprachlich etwas glatter.
Zu Variante 2a von Nummero6/TchuTcha Tcha
Gut, nur ein Tippfehler: Statt "für die Schenkel gilt" meinten Sie sicher "für die Winkel gilt".
--Buchner 10:47, 17. Jun. 2012 (CEST)
Variante 1b
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn ein Schenkel identisch ist und die beiden anderen Schenkel eine Gerade bilden.
Definition von Snooth
Definition
(Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn sie einen gemeinsamen Schenkel besitzen und sie sich zu 180° ergänzen, d.h. supplementär sind.
--Snooth 15:49, 14. Jun. 2012 (CEST)
Bemerkung M.G.
- Wäre prinzipiell korrekt, ist jedoch nicht zu unserem Aufbau der Geometrie kompatibel. Wir klären erst Nebenwinkel und dann supplementär. Für unseren Aufbau der Geometrie ist eine Definition besser, die nicht auf die 180° Bezug nimmt.--*m.g.* 17:05, 16. Jun. 2012 (CEST)
zurück zu: Winkel SS 2012

