Lösung von Aufgabe 9.3 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „ '''Satz:'''<br /> '''Es sei <math>g</math> eine Gerade der Ebene <math>E</math>. Ferner sei <math>P</math> ein Punkt auf <math>g</math>. In der Ebene <math>E</ma…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | |||
'''Satz:'''<br /> | '''Satz:'''<br /> | ||
'''Es sei <math>g</math> eine Gerade der Ebene <math>E</math>. Ferner sei <math>P</math> ein Punkt auf <math>g</math>. In der Ebene <math>E</math> gibt es genau eine Gerade <math>s</math>, die durch <math>P</math> geht und senkrecht auf <math>g</math> steht.'''<br /> | '''Es sei <math>g</math> eine Gerade der Ebene <math>E</math>. Ferner sei <math>P</math> ein Punkt auf <math>g</math>. In der Ebene <math>E</math> gibt es genau eine Gerade <math>s</math>, die durch <math>P</math> geht und senkrecht auf <math>g</math> steht.'''<br /> | ||
Beweisen Sie den Satz.<br /> | Beweisen Sie den Satz.<br /> | ||
| − | <br /> | + | <br />Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> |
| + | [[Datei:Aufgabe 9.3S.png]]<br />Eindeutigkeitsbeweis..Beweisen durch Widerspruch!<br />Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.<br />Fortsetzung folgt...--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 16:56, 20. Jun. 2012 (CEST) | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Version vom 20. Juni 2012, 15:56 Uhr
Satz:
Es sei 
eine Gerade der Ebene 
. Ferner sei 
ein Punkt auf . In der Ebene gibt es genau eine Gerade 
, die durch geht und senkrecht auf steht.
Beweisen Sie den Satz.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
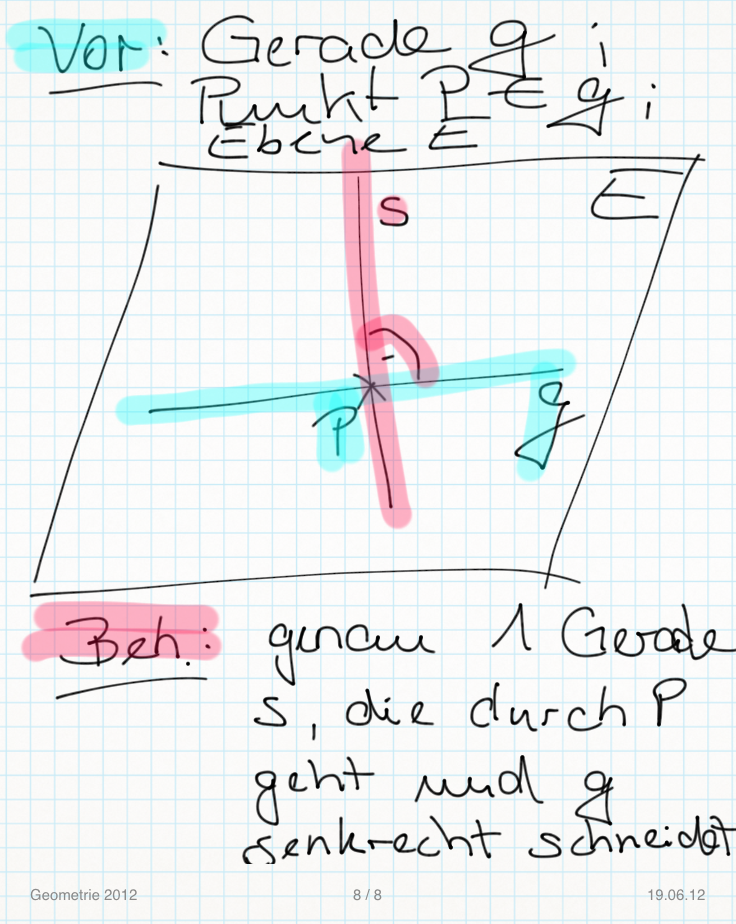
Eindeutigkeitsbeweis..Beweisen durch Widerspruch!
Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.
Fortsetzung folgt...--Tchu Tcha Tcha 16:56, 20. Jun. 2012 (CEST)
