Lösung von Aufgabe 9.3 S: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bemerkung M.G.) |
|||
| Zeile 4: | Zeile 4: | ||
Beweisen Sie den Satz.<br /> | Beweisen Sie den Satz.<br /> | ||
| − | ==Lösungsversuch Nummero6/Tchu Tcha Tcha:== | + | ==Lösungsversuch 1 Nummero6/Tchu Tcha Tcha:== |
[[Datei:Aufgabe 9.3S.png]]<br />Eindeutigkeitsbeweis..Beweisen durch Widerspruch!<br />Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.<br />Fortsetzung folgt...<br /> | [[Datei:Aufgabe 9.3S.png]]<br />Eindeutigkeitsbeweis..Beweisen durch Widerspruch!<br />Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.<br />Fortsetzung folgt...<br /> | ||
Könnte man hier nicht einen Widerspruchsbeweis mit dem Winkelkonstruktionsaxiom führen?? | Könnte man hier nicht einen Widerspruchsbeweis mit dem Winkelkonstruktionsaxiom führen?? | ||
| Zeile 13: | Zeile 13: | ||
===Bemerkung M.G.=== | ===Bemerkung M.G.=== | ||
Richtig, Eindeutigkeitsbeweise führt man in der Regel indirekt. Wir nehmen an, es gäbe zwei Geraden <math>s_1</math> und <math>s_2</math>, die beide durch <math>P</math> gehen und senkrecht auf <math>g</math> stehen. Senkrecht stehen bedeutet, dass rechte Winkel gebildet werden. Jeder rechte Winkel hat das maß 90° ... . Sie haben den Beweis schon völlig verstanden. Was Ihnen wahrscheinlich Schwierigkeiten bereitet, ist das Aufschreiben desselben. Hilfe: Führen Sie auf <math>g, s_1</math> und <math>s_2</math> geeignete Punkte ein. Dann können Sie die entstehenden rechten Winkel besser bezeichnen. Danach wird Ihnen das Winkelkonstruktionsaxiom wacker zur Seite stehen.--[[Benutzer:*m.g.*|*m.g.*]] 10:04, 24. Jun. 2012 (CEST) | Richtig, Eindeutigkeitsbeweise führt man in der Regel indirekt. Wir nehmen an, es gäbe zwei Geraden <math>s_1</math> und <math>s_2</math>, die beide durch <math>P</math> gehen und senkrecht auf <math>g</math> stehen. Senkrecht stehen bedeutet, dass rechte Winkel gebildet werden. Jeder rechte Winkel hat das maß 90° ... . Sie haben den Beweis schon völlig verstanden. Was Ihnen wahrscheinlich Schwierigkeiten bereitet, ist das Aufschreiben desselben. Hilfe: Führen Sie auf <math>g, s_1</math> und <math>s_2</math> geeignete Punkte ein. Dann können Sie die entstehenden rechten Winkel besser bezeichnen. Danach wird Ihnen das Winkelkonstruktionsaxiom wacker zur Seite stehen.--[[Benutzer:*m.g.*|*m.g.*]] 10:04, 24. Jun. 2012 (CEST) | ||
| − | + | <br /> | |
| + | Lösungsversuch 2 Nummero6/Tchu Tcha Tcha:<br /> | ||
| + | Annahme: Es gibt 2 Geraden <math>s_1</math> und <math>s_2</math>, die beide durch <math>P</math> gehen und senkrecht auf <math>g</math> stehen.<br /> | ||
| + | (1) <math>g\in E</math> // Voraussetzung<br /> | ||
| + | (2) <math>P\in g</math> // Voraussetzung<br /> | ||
| + | (3) <math>\exists s_1 \in E: s_1\cap g = \{P\} \wedge s_1 \perp g</math> //Annahme<br /> | ||
| + | (4) <math>\exists s_2 \in E: s_2\cap g = \{P\} \wedge s_2 \perp g</math> //Annahme<br /> | ||
| + | (5) <math>\exists S_1 \in s_1 \wedge S_2 \in s_2 \wedge P_2 \in g</math>: <math>S_1\neq S_2\neq P_2\neq P\neq S_1</math> // Axiom I.2<br /> | ||
| + | (6) <math>\left|\angle S_1PP_2\right| = 90 \wedge \left|\angle S_2PP_2\right| = 90</math> // Annahme, (3),(4)<br /> | ||
| + | (7) Nach dem Winkelkonstruktionsaxiom gibt es genau 1 Strahl <math>\ PS^{+}</math> zu <math>\ PP_2</math>mit der Größe 90. Nach (6) müssen die Strahlen | ||
| + | <math>\ PS_1^{+}</math> und <math>\ PS_2^{+}</math> identisch sein.<br /> | ||
| + | (8) Widerspruch zur Annahme! // (7)<br /> | ||
| + | (9) Behauptung stimmt! // (8)<br /> | ||
| + | qed<br /> | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:23, 24. Jun. 2012 (CEST) | ||
| + | <br /> | ||
==Lösung von Ritterport== | ==Lösung von Ritterport== | ||
<br /><u>'''Idee:''' (Wir sind in einer Ebene E)<br /></u> | <br /><u>'''Idee:''' (Wir sind in einer Ebene E)<br /></u> | ||
Version vom 24. Juni 2012, 18:23 Uhr
Inhaltsverzeichnis |
Die Aufgabe
Satz
Es sei  eine Gerade der Ebene
eine Gerade der Ebene  . Ferner sei
. Ferner sei  ein Punkt auf
ein Punkt auf  . In der Ebene
. In der Ebene  gibt es genau eine Gerade
gibt es genau eine Gerade  , die durch
, die durch  geht und senkrecht auf
geht und senkrecht auf  steht.
steht.
Beweisen Sie den Satz.
Lösungsversuch 1 Nummero6/Tchu Tcha Tcha:
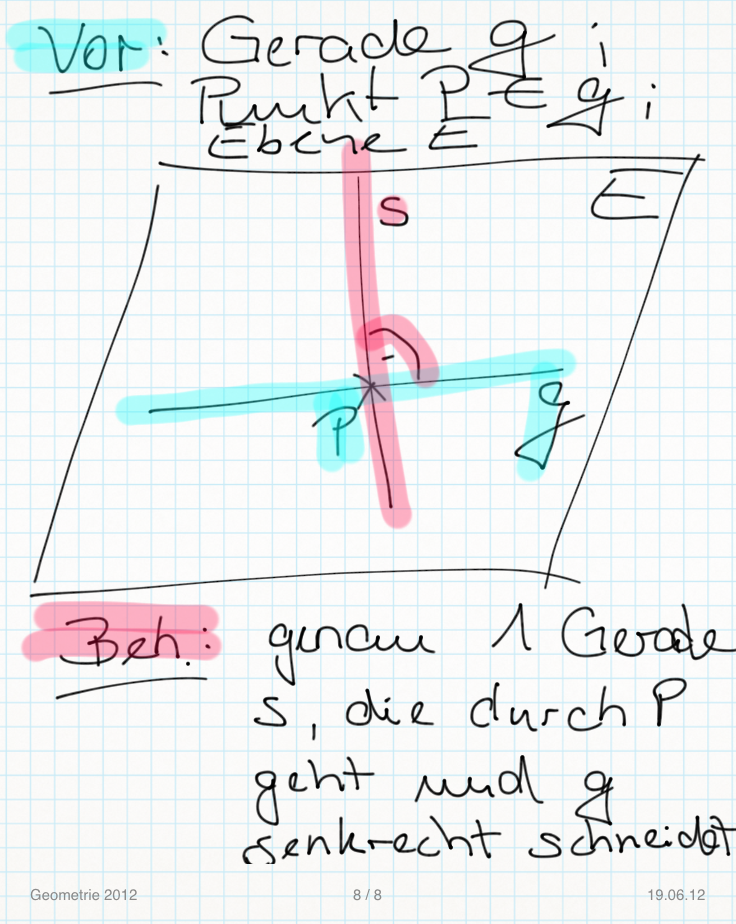
Eindeutigkeitsbeweis..Beweisen durch Widerspruch!
Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.
Fortsetzung folgt...
Könnte man hier nicht einen Widerspruchsbeweis mit dem Winkelkonstruktionsaxiom führen??
Letztendlich wird dann gesagt, dass es ein Widerspruch zu diesem Axiom wäre, da es nur genau einen Strahl in der Halbebene gibt, der das Maß 90 hat..?!?
 die 2 Geraden müssten identisch sein, also Widerspruch zur Annahme! Behauptung stimmt..
die 2 Geraden müssten identisch sein, also Widerspruch zur Annahme! Behauptung stimmt..
--Tchu Tcha Tcha 16:56, 20. Jun. 2012 (CEST)
Bemerkung M.G.
Richtig, Eindeutigkeitsbeweise führt man in der Regel indirekt. Wir nehmen an, es gäbe zwei Geraden 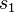 und
und 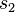 , die beide durch
, die beide durch  gehen und senkrecht auf
gehen und senkrecht auf  stehen. Senkrecht stehen bedeutet, dass rechte Winkel gebildet werden. Jeder rechte Winkel hat das maß 90° ... . Sie haben den Beweis schon völlig verstanden. Was Ihnen wahrscheinlich Schwierigkeiten bereitet, ist das Aufschreiben desselben. Hilfe: Führen Sie auf
stehen. Senkrecht stehen bedeutet, dass rechte Winkel gebildet werden. Jeder rechte Winkel hat das maß 90° ... . Sie haben den Beweis schon völlig verstanden. Was Ihnen wahrscheinlich Schwierigkeiten bereitet, ist das Aufschreiben desselben. Hilfe: Führen Sie auf 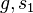 und
und 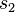 geeignete Punkte ein. Dann können Sie die entstehenden rechten Winkel besser bezeichnen. Danach wird Ihnen das Winkelkonstruktionsaxiom wacker zur Seite stehen.--*m.g.* 10:04, 24. Jun. 2012 (CEST)
geeignete Punkte ein. Dann können Sie die entstehenden rechten Winkel besser bezeichnen. Danach wird Ihnen das Winkelkonstruktionsaxiom wacker zur Seite stehen.--*m.g.* 10:04, 24. Jun. 2012 (CEST)
Lösungsversuch 2 Nummero6/Tchu Tcha Tcha:
Annahme: Es gibt 2 Geraden 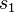 und
und 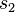 , die beide durch
, die beide durch  gehen und senkrecht auf
gehen und senkrecht auf  stehen.
stehen.
(1) 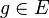 // Voraussetzung
// Voraussetzung
(2) 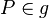 // Voraussetzung
// Voraussetzung
(3) 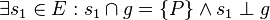 //Annahme
//Annahme
(4) 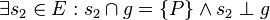 //Annahme
//Annahme
(5) 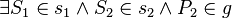 :
: 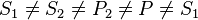 // Axiom I.2
// Axiom I.2
(6) 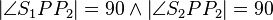 // Annahme, (3),(4)
// Annahme, (3),(4)
(7) Nach dem Winkelkonstruktionsaxiom gibt es genau 1 Strahl 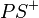 zu
zu 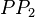 mit der Größe 90. Nach (6) müssen die Strahlen
mit der Größe 90. Nach (6) müssen die Strahlen
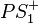 und
und 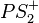 identisch sein.
identisch sein.
(8) Widerspruch zur Annahme! // (7)
(9) Behauptung stimmt! // (8)
qed
--Tchu Tcha Tcha 19:23, 24. Jun. 2012 (CEST)
Lösung von Ritterport
Idee: (Wir sind in einer Ebene E)
Es gibt einen Punkt  , der nicht auf
, der nicht auf  liegt. Die Gerade
liegt. Die Gerade  geht durch
geht durch  und
und  . (Axiom I.1)
. (Axiom I.1)
Also: 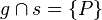
Winkel 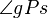 hat das Maß
hat das Maß 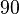 (Es gibt rechte Winkel, Axiom W.4 --> Alle vier Winkel um P haben das Maß 90)
(Es gibt rechte Winkel, Axiom W.4 --> Alle vier Winkel um P haben das Maß 90)
--> Eindeutigkeit und Existenz bewiesen. (!?)
--RitterSport 19:50, 23. Jun. 2012 (CEST)
Bemerkung M.G.
Sie verwenden einen beliebigen Punkt  außerhalb von
außerhalb von  . Das ist Ihr gutes Recht und auch nach den Axiomen der absoluten Geometrie zulässig. Die beiden Punkte
. Das ist Ihr gutes Recht und auch nach den Axiomen der absoluten Geometrie zulässig. Die beiden Punkte  und
und  bestimmen jetzt eindeutig eine Gerade, was natürlich entsprechend I/1 gilt. Warum sollte diese Gerade jetzt aber mit der Geraden
bestimmen jetzt eindeutig eine Gerade, was natürlich entsprechend I/1 gilt. Warum sollte diese Gerade jetzt aber mit der Geraden  rechte Winkel bilden? Der Punkt
rechte Winkel bilden? Der Punkt  war beliebig in unserer Ebene gewählt. Einzige Bedingung war, dass er nicht auf
war beliebig in unserer Ebene gewählt. Einzige Bedingung war, dass er nicht auf  liegen sollte. Da bedarf es schon einer gehörigen Portion Glück, den Punkt
liegen sollte. Da bedarf es schon einer gehörigen Portion Glück, den Punkt  derart gewählt zu haben, dass
derart gewählt zu haben, dass 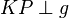 gilt.
gilt.
Was hilft wirklich? Wir wissen, dass wir einen Winkel mit dem Maß 90° bräuchten. Dieser sollte  als Scheitelpunkt haben und eine der beiden Halbgeraden von
als Scheitelpunkt haben und eine der beiden Halbgeraden von  , die durch
, die durch  eindeutig bestimmt sind, als Schenkel verwenden.
eindeutig bestimmt sind, als Schenkel verwenden.
Fangen wir doch einfach mit einer dieser Halbgeraden an: Es sei 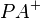 eine der beiden Halbgeraden, die durch
eine der beiden Halbgeraden, die durch  auf
auf  eindeutig bestimmt sind. Das Winkelkonstruktionsaxiom liefert uns jetzt ...
eindeutig bestimmt sind. Das Winkelkonstruktionsaxiom liefert uns jetzt ...
Wenn wir damit fertig sind, haben wir die Existenz einer in  auf
auf  senkrecht stehenden Geraden
senkrecht stehenden Geraden  bewiesen. Was bleibt ist die Eindeutigkeit. S. oben Tchu Tcha Tcha
--*m.g.* 10:21, 24. Jun. 2012 (CEST)
bewiesen. Was bleibt ist die Eindeutigkeit. S. oben Tchu Tcha Tcha
--*m.g.* 10:21, 24. Jun. 2012 (CEST)

