Lösung von Aufg. 10.3 S: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Kopernikus / Just noch ein sailA)
(→‎Kopernikus / Just noch ein sailA)
Zeile 44: Zeile 44:
 
--[[Benutzer:Kopernikus|Kopernikus]] 15:21, 28. Jun. 2012 (CEST)<br />
 
--[[Benutzer:Kopernikus|Kopernikus]] 15:21, 28. Jun. 2012 (CEST)<br />
 
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 15:21, 28. Jun. 2012  (CEST)<br /><br />
 
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 15:21, 28. Jun. 2012  (CEST)<br /><br />
 +
<br />
 +
Lösungsversuch Nummero6/Tchu Tcha Tcha:<br />
 +
Vor.: <math>P \in m_AB</math><br />
 +
Beh.: <math>\left| PA \right| = \left| PB \right|</math><br />
 +
 +
(1) <math>\left| AM \right| kongruent \left| MB \right|</math> // Vor., Def. Mittelsenkrechte<br />
 +
(2) <math>\left| MP \right| =\left| MP \right|</math> // trivial<br />
 +
(3) <math>\left| \angle AMP  \right| = \left| \angle BMP  \right|</math> // Vor., Def. Mittelsenkrechte<br />
 +
(4) <math>\overline{AMP} = \overline{BMP} // (1-3), SWS</math><br />
 +
(5) <math>\left| PA \right| = \left| PB \right|</math> // (4), Dreieckskongruenz<br />
 +
qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:24, 30. Jun. 2012 (CEST)
  
 
==  ==
 
==  ==

Version vom 30. Juni 2012, 11:24 Uhr

Kopernikus / Just noch ein sailA

Beweisen Sie Satz VII.6 b

Wenn ein Punkt \ P zur Mittelsenkrechten der Strecke \overline{AB} gehört, dann hat er zu den Punkten \ A und \ B ein und denselben Abstand.

Vor:
1. 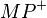\ MP^{+} ist Mittelsenkrechte von \overline{AB}
2. \overline{AB}
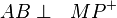
3. \ AB \perp \ \ MP^{+}

Beh:
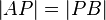
\left| AP \right| =\left| PB \right|

Schritt Beweis Begründung
1 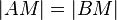\left| AM \right| =\left| BM \right| Vor; Def. Mittelsenkrechte.
2 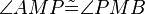\angle AMP \tilde {=} \angle PMB Axiom IV.4, Def. V.7
3 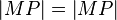\left| MP \right| =\left| MP \right| trivial
4 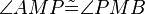\angle AMP \tilde {=} \angle PMB Axiom V, SWS
5 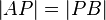\left| AP \right| =\left| PB \right|


--Kopernikus 15:21, 28. Jun. 2012 (CEST)
--Just noch ein sailA 15:21, 28. Jun. 2012 (CEST)


Lösungsversuch Nummero6/Tchu Tcha Tcha:
Vor.: 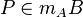P \in m_AB
Beh.: 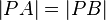\left| PA \right| = \left| PB \right|

(1) 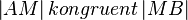\left| AM \right| kongruent \left| MB \right| // Vor., Def. Mittelsenkrechte
(2) 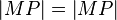\left| MP \right| =\left| MP \right| // trivial
(3) 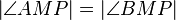\left| \angle AMP \right| = \left| \angle BMP \right| // Vor., Def. Mittelsenkrechte
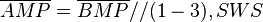
(4) \overline{AMP} = \overline{BMP} // (1-3), SWS
(5) 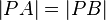\left| PA \right| = \left| PB \right| // (4), Dreieckskongruenz
qed
--Tchu Tcha Tcha 12:24, 30. Jun. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._10.3_S&oldid=15683“