Lösung von Zusatzaufgabe 10.1 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br /> a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.<br /> Wenn in einem Dr…“) |
|||
| Zeile 1: | Zeile 1: | ||
Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br /> | Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br /> | ||
a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.<br /> | a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.<br /> | ||
| − | Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:55, 30. Jun. 2012 (CEST) | + | Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.<br /> |
| + | |||
| + | b) Vor. <math>a \tilde {=} c</math> <br /> | ||
| + | Beh.: <math>\alpha \tilde {=} \beta</math> .. hier: <br /> | ||
| + | |||
| + | (1) <math>a \tilde {=} c</math> // Vor. <br /> | ||
| + | (2) es existiert w (die WH von <math>\gamma</math>) // Ex. & Eind. der WH<br /> | ||
| + | (3) <math>\ w \cap \overline{AB} = \{S}</math> // Vor., (1), Lemma 1<br /> | ||
| + | (4) <math>\left| \angle ACS \right| \tilde {=} \left| \angle DCS \right| \tilde</math> // (2),(3)<br /> | ||
| + | (5) <math>\overline{CS} \tilde {=} \overline{CS}</math> // trivial, Vor., (3)<br /> | ||
| + | (6) <math>\overline{ACS} = \overline{ACS}</math> // (1),(4),(5), SWS<br /> | ||
| + | (7) <math>\angle SAC \tilde {=} \angle SBC</math> // (6), Dreieckskongruenz<br /> | ||
| + | (8) Beh. stimmt // (7)<br /> | ||
| + | qed<br /> | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:55, 30. Jun. 2012 (CEST) | ||
Version vom 30. Juni 2012, 12:17 Uhr
Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:
a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.
Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.
b) Vor.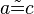 
Beh.: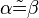 
.. hier:
(1) 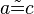// Vor.
(2) es existiert w (die WH von 
) // Ex. & Eind. der WH
(3) Fehler beim Parsen(Syntaxfehler): \ w \cap \overline{AB} = \{S}
// Vor., (1), Lemma 1
(4) Fehler beim Parsen(Syntaxfehler): \left| \angle ACS \right| \tilde {=} \left| \angle DCS \right| \tilde
// (2),(3)
(5) 
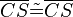// trivial, Vor., (3)
(6) 
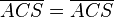// (1),(4),(5), SWS
(7) 
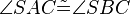// (6), Dreieckskongruenz
(8) Beh. stimmt // (7)
qed
--Tchu Tcha Tcha 12:55, 30. Jun. 2012 (CEST)
