Lösung von Aufgabe 6.8: Unterschied zwischen den Versionen
(→Kreisdurchmesser) |
|||
| Zeile 14: | Zeile 14: | ||
==== Kreisdurchmesser ==== | ==== Kreisdurchmesser ==== | ||
Eine Kreisdurchmesser ist die Strecke (Verbindung) zwischen zwei Punkten P<sub>l</sub> und P<sub>m</sub>, die durch den Mittelpunkt geht. | Eine Kreisdurchmesser ist die Strecke (Verbindung) zwischen zwei Punkten P<sub>l</sub> und P<sub>m</sub>, die durch den Mittelpunkt geht. | ||
| − | Da es sich also um die addierten Strecken <math>\overline { | + | Da es sich also um die addierten Strecken <math>\overline {P_lM} und \overline {P_mM}</math> handelt, ist der Durchmesser immer = doppelter Radius. Echt. |
<br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] | <br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] | ||
Version vom 4. Juni 2010, 02:38 Uhr
Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.
Nochmal zur Erklärung die Kreisdefinition aus Aufgabe 6.7:
Ein Kreis sei die Menge aller Punkte Pi, die den gleichen Abstand zu Punkt M haben. Diesen Punkt M nennen wir Mittelpunkt des Kreises.
Vorraussetzung: Alle Punkte Pi und der Punkt M liegen in der selben Ebene 
.
Kreissehnen
Eine Kreissehne ist die Strecke (Verbindung) zwischen zwei Punkten des Kreises: Pj und Pk
Kreisradien
Eine Kreisradius ist die Strecke (Verbindung) zwischen dem Mittelpunkt M des Kreises und einem beliebigen Punkt Pi. (geht mit allen Ps, da Definition Kreis sagt, dass Kreis durch GLEICHEN Abstand definiert ist.
Kreisdurchmesser
Eine Kreisdurchmesser ist die Strecke (Verbindung) zwischen zwei Punkten Pl und Pm, die durch den Mittelpunkt geht.
Da es sich also um die addierten Strecken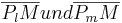 
handelt, ist der Durchmesser immer = doppelter Radius. Echt.
