Lösung von Testaufgabe 02: Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
<br/> | <br/> | ||
Hier meine Idee: <br/> | Hier meine Idee: <br/> | ||
| − | [[Datei:RitterSport_Foto0169.jpg]]--[[Benutzer:RitterSport|RitterSport]] 21: | + | [[Datei:RitterSport_Foto0169.jpg]]<br/> |
| + | --[[Benutzer:RitterSport|RitterSport]] 21:20, 9. Jul. 2012 (CEST) | ||
Version vom 9. Juli 2012, 20:20 Uhr
Lösungsversuch Nummero6/Tchu Tcha Tcha:
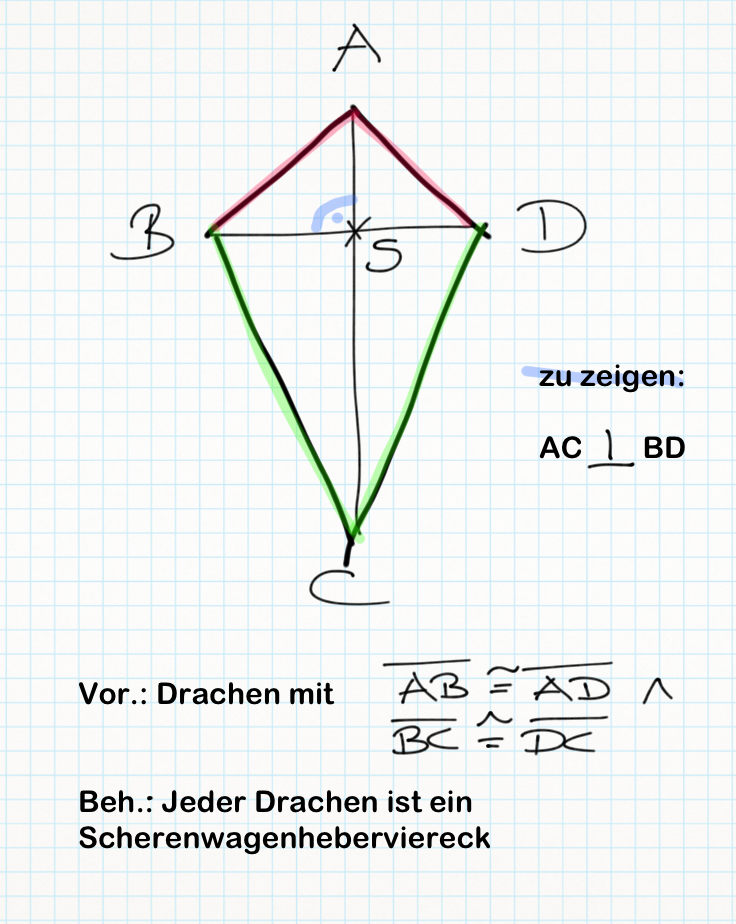
(1) 
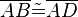// Vor.
(2) 
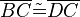// Vor.
(3) 
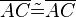// Vor.
(4) 
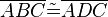// (1-3), SSS
(5) 
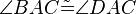// (4), Dreieckskongruenz
(6) 
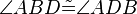// Vor., Basiswinkelsatz
(7) 
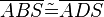// (5),(1),(6), WSW
(8) 
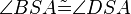// (7), Dreieckskongruenz
(9) 
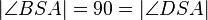// (8), Def.NW, Def. rechter Winkel
(10) Da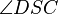 
Nebenwinkel von 
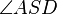und 
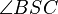Nebenwinkel von 
ist,
muss nach Def. NW und Def. rechter Winkel gelten: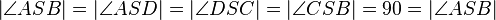 
(11) Nach (10) und der Def. senkrecht auf der Menge der Geraden bzw. Strecken wissen wir nun:
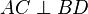
(12) Nach der "Def. Scherenwagenheberviereck" ist auch jeder Drachen wegen (11) ein Scherenwagenheberviereck.
(13) Behauptung stimmt. qed. // (12)
(Hinweis:10 Minuten waren mir mit Zeichnung zu knapp.. eher 15 min :-( )
--Tchu Tcha Tcha 22:02, 8. Jul. 2012 (CEST)
Hier meine Idee:
--RitterSport 21:20, 9. Jul. 2012 (CEST)
