Sätze über Dreiecke (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“) |
K (→Satz XII.5: (Starker Außenwinkelsatz)) |
||
| Zeile 12: | Zeile 12: | ||
===== Satz XII.5: (Starker Außenwinkelsatz) ===== | ===== Satz XII.5: (Starker Außenwinkelsatz) ===== | ||
| − | :: Jeder Außenwinkel eines Dreiecks ist so groß, wie die Summe der | + | :: Jeder Außenwinkel eines Dreiecks ist so groß, wie die Summe der Größen der beiden nicht anliegenden Innenwinkel dieses Dreiecks. |
| + | |||
===== Beweis von Satz XII.5: (Starker Außenwinkelsatz) ===== | ===== Beweis von Satz XII.5: (Starker Außenwinkelsatz) ===== | ||
Übungsaufgabe | Übungsaufgabe | ||
Aktuelle Version vom 10. Juli 2012, 12:35 Uhr
|
Satz XII.4: (Innenwinkelsatz für Dreiecke)
Beweis von Satz XII.4 (Innenwinkelsatz für Dreiecke)Übungsaufgabe Satz XII.5: (Starker Außenwinkelsatz)
Beweis von Satz XII.5: (Starker Außenwinkelsatz)Übungsaufgabe
|
ein Dreieck mit den Innenwinkeln 
, 
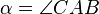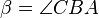und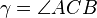 
. 
.
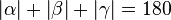