Lösung von Aufgabe 11.3P (SoSe 12): Unterschied zwischen den Versionen
| Zeile 9: | Zeile 9: | ||
Der zweite Teil mit der Begründung der Achsenkonstruktion ist korrekt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 09:01, 10. Jul. 2012 (CEST) | Der zweite Teil mit der Begründung der Achsenkonstruktion ist korrekt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 09:01, 10. Jul. 2012 (CEST) | ||
Man kann den Kreis konstruieren, in dem man A mit A' und B mit B' verbindet, da den Mittelpunkt rausfindet und den Zirkel an der Stelle einsticht. | Man kann den Kreis konstruieren, in dem man A mit A' und B mit B' verbindet, da den Mittelpunkt rausfindet und den Zirkel an der Stelle einsticht. | ||
| − | --[[Benutzer:WG-Hoffut|WG-Hoffut]] 11:41, 11. Jul. 2012 (CEST) | + | --[[Benutzer:WG-Hoffut|WG-Hoffut]] 11:41, 11. Jul. 2012 (CEST)<br /> |
| + | Du konstruierst also Halbkreise - aber warum sollte der Schnittpunkt der Halbkreise nun der Drehpunkt sein?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:16, 12. Jul. 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 12. Juli 2012, 10:16 Uhr
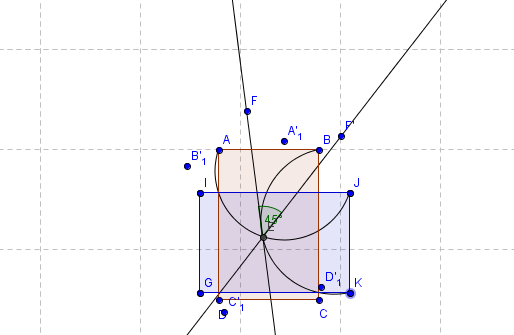
Das Rechteck  soll durch eine Drehung auf das blaue Rechteck abgebildet werden. Konstruieren Sie den Drehpunkt. Wo müssen die beiden Achsen liegen, wenn die Drehung durch eine Verkettung zweier Achsenspiegelungen erzeugt werden soll?
soll durch eine Drehung auf das blaue Rechteck abgebildet werden. Konstruieren Sie den Drehpunkt. Wo müssen die beiden Achsen liegen, wenn die Drehung durch eine Verkettung zweier Achsenspiegelungen erzeugt werden soll?
Wir haben einen Kreis konstruiert, auf dem die Punkte A und (hier) J liegen ebenso für die Punkte B und (hier) K. Der Schnittpunkt E ist der gesuchte Drehpunkt. Anschließend haben wir einen beliegen Punkt F gewählt und eine Gerade durch diesen und den Punkt E gezogen. Dies ist unsere erste Spiegelachse. Da die Drehung 90° beträgt, haben wir nach Satz IX.2 einen Winkel von 45° zwischen den Spiegelgeraden gewählt. Somit ist die zweite Spiegelgerade entstanden.
Als Test spiegelten wir die Punkte A,B,C,D an den kontruierten Spiegelachsen. A wurde durch die Verkettung der beiden Spiegelgeraden auf J abgebildet, B auf K, C auf G und D auf I.
--WG-Hoffut 17:28, 7. Jul. 2012 (CEST)
Wie kannst du durch zwei Punkte genau einen Kreis konstruieren?
Der zweite Teil mit der Begründung der Achsenkonstruktion ist korrekt.--Tutorin Anne 09:01, 10. Jul. 2012 (CEST)
Man kann den Kreis konstruieren, in dem man A mit A' und B mit B' verbindet, da den Mittelpunkt rausfindet und den Zirkel an der Stelle einsticht.
--WG-Hoffut 11:41, 11. Jul. 2012 (CEST)
Du konstruierst also Halbkreise - aber warum sollte der Schnittpunkt der Halbkreise nun der Drehpunkt sein?--Tutorin Anne 11:16, 12. Jul. 2012 (CEST)
Verbinde A mit A`und B mit B`. Zeichne die Mittelsenkrechten der Strecken AA´und BB`. Du erhälst den Schnittpunkt P der beiden Mittelsenkrechten. P ist Drehpunkt mit dem Drehwinkel 90°.--Geogeogeo 13:59, 9. Jul. 2012 (CEST)
So ist es!--Tutorin Anne 09:01, 10. Jul. 2012 (CEST)
--Studentin 15:55, 1. Jul. 2012 (CEST)
--Studentin 16:02, 1. Jul. 2012 (CEST)
alle guten dinge sind drei, jetzt sind die spiegelachsen fixiert und punkt e kann verändert werden:
--Studentin 16:16, 1. Jul. 2012 (CEST)
top! es genügen 2 Mittelsenkrechten zur Konstruktion.--Tutorin Anne 20:13, 5. Jul. 2012 (CEST)