Lösung von Aufgabe 7.10: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.) |
Nicola (Diskussion | Beiträge) (table+) |
||
| Zeile 1: | Zeile 1: | ||
| − | |||
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt. | Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt. | ||
| + | |||
| + | |||
| + | |||
| + | A--M--B | ||
| + | |||
| + | Voraussetzung: koll(A, M, B), zw (A, M, B), <math>\overline{AM}</math> = <math>\overline{MB}</math> | ||
| + | |||
| + | zu zeigen: Es gibt nur einen Punkt M, auf den die o.g. Sachverhalte zutreffen. | ||
| + | |||
| + | M = Mittelpunkt, da | ||
| + | Definition III.1: (Mittelpunkt einer Strecke) | ||
| + | |||
| + | <math>\overline{AM}</math> ist eindeutig für <math>\overline{AB}</math> definiert | ||
| + | Axiom II.1: (Abstandsaxiom) | ||
Version vom 6. Juni 2010, 14:41 Uhr
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
A--M--B
Voraussetzung: koll(A, M, B), zw (A, M, B), 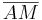 =
= 
zu zeigen: Es gibt nur einen Punkt M, auf den die o.g. Sachverhalte zutreffen.
M = Mittelpunkt, da Definition III.1: (Mittelpunkt einer Strecke)
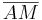 ist eindeutig für
ist eindeutig für  definiert
Axiom II.1: (Abstandsaxiom)
definiert
Axiom II.1: (Abstandsaxiom)

