Lösung von Aufg. 12.4 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Es sei folgende Definition für den Begriff ''Parallelogramm'' gegeben:<br /> ::Definition 1: Ein Viereck mit zwei Paaren paralleler Seiten heißt Parallelogramm.…“) |
|||
| Zeile 2: | Zeile 2: | ||
::Definition 1: Ein Viereck mit zwei Paaren paralleler Seiten heißt Parallelogramm.<br /> | ::Definition 1: Ein Viereck mit zwei Paaren paralleler Seiten heißt Parallelogramm.<br /> | ||
'''Beweisen Sie:''' Wenn sich in einem Viereck die Diagonalen halbieren, dann ist das Viereck ein Parallelogramm (entsprechend Definition 1).<br /> | '''Beweisen Sie:''' Wenn sich in einem Viereck die Diagonalen halbieren, dann ist das Viereck ein Parallelogramm (entsprechend Definition 1).<br /> | ||
| + | <br /> | ||
| + | Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> | ||
| + | [[Datei:Übung 12.4.png]] | ||
| + | <br /> | ||
| + | (1) <math>\left| AM \right| = \left| MC \right|</math> // Vor.<br /> | ||
| + | (2) <math>\left| BM \right| = \left| MD \right|</math> // Vor.<br /> | ||
| + | (3) <math>\alpha \tilde {=} \alpha'</math> // kongruente Scheitelwinkel<br /> | ||
| + | (4) <math>\beta \tilde {=} \beta'</math> // kongruente Scheitelwinkel<br /> | ||
| + | (5) <math>\overline{AMB} \tilde {=} \overline{CMD}</math> // (1-3), SWS<br /> | ||
| + | (6) <math>\gamma \tilde {=} \gamma'</math> // (5), Dreieckskongruenz<br /> | ||
| + | (7) a parallel c // (6), Umkehrung Wechselwinkelsatz<br /> | ||
| + | -analog für <math>\overline{AMD} \tilde {=} \overline{BMC}</math>-<br /> | ||
| + | -b parallel d-<br /> | ||
| + | qed.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 22:55, 12. Jul. 2012 (CEST) | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 12. Juli 2012, 21:55 Uhr
Es sei folgende Definition für den Begriff Parallelogramm gegeben:
- Definition 1: Ein Viereck mit zwei Paaren paralleler Seiten heißt Parallelogramm.
- Definition 1: Ein Viereck mit zwei Paaren paralleler Seiten heißt Parallelogramm.
Beweisen Sie: Wenn sich in einem Viereck die Diagonalen halbieren, dann ist das Viereck ein Parallelogramm (entsprechend Definition 1).
Lösungsversuch Nummero6/Tchu Tcha Tcha:
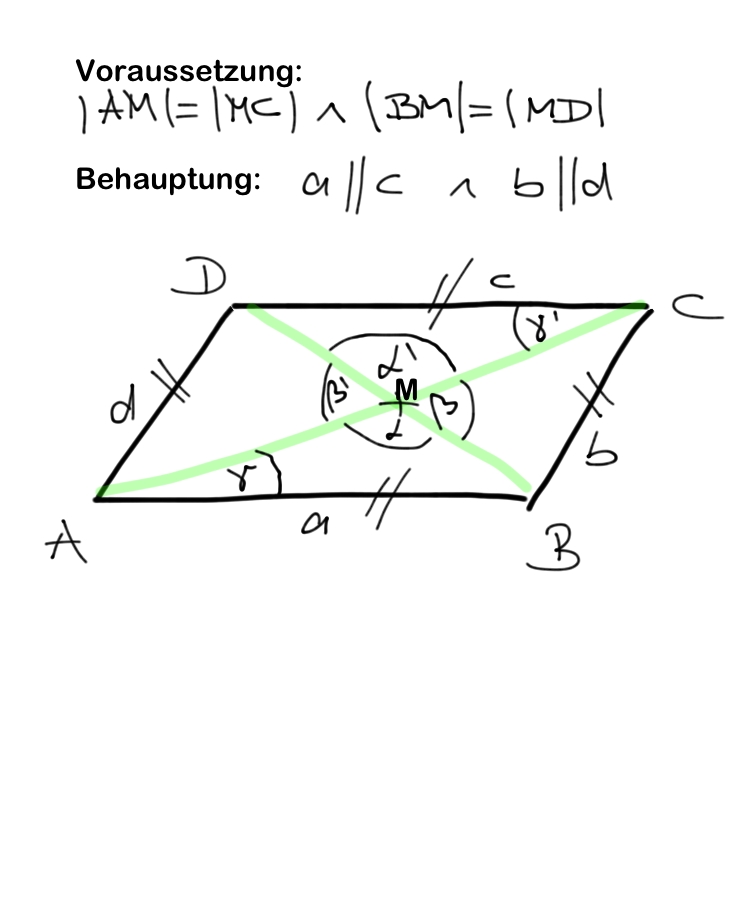
(1) 
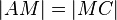// Vor.
(2) 
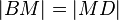// Vor.
(3) 
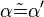// kongruente Scheitelwinkel
(4) 
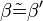// kongruente Scheitelwinkel
(5) 
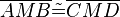// (1-3), SWS
(6) 
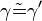// (5), Dreieckskongruenz
(7) a parallel c // (6), Umkehrung Wechselwinkelsatz
-analog für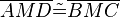 
-
-b parallel d-
qed.
--Tchu Tcha Tcha 22:55, 12. Jul. 2012 (CEST)
